“กรวย” ก็เป็นหนึ่งในรูปทรงที่สำคัญมาก ๆ สำหรับน้อง ๆ ม. 3 ทุกคนที่มีโอกาสได้เรียนเรื่องการหาพื้นที่และปริมาตรของรูปทรงเรขาคณิตสามมิติ เนื่องจากเป็นหนึ่งในรูปทรงที่พบเห็นในชีวิตประจำวันค่อนข้างบ่อย และออกข้อสอบบ่อยที่สุดรูปหนึ่ง ทั้งข้อสอบในโรงเรียนและข้อสอบเข้าม.4 โรงเรียนต่าง ๆ ดังนั้นแล้ว พี่ ๆ ATHOME จึงอยากจะชวนให้น้อง ๆ มาทบทวนและตะลุยแบบฝึกหัดไปพร้อมกัน เพื่อเป็นการอุดรูรั่วส่วนที่น้องยังไม่แม่น เพื่อเตรียมไปพิชิตสนามสอบ
รู้จัก ทรงกรวย
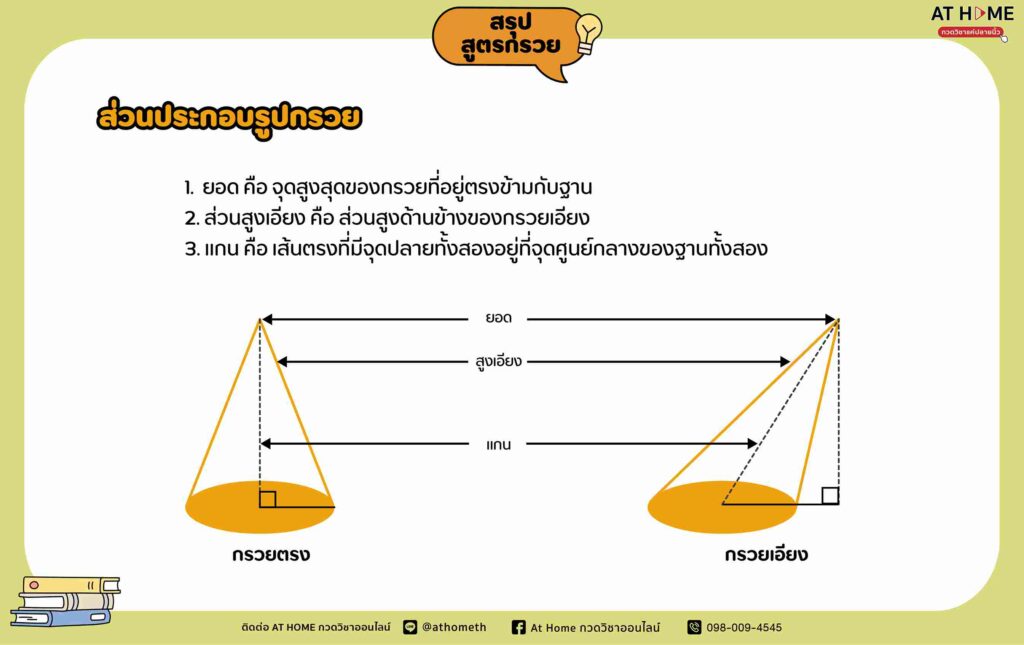
สูตรหาปริมาตรกรวย
สูตรหาพื้นที่ทรงกรวย

ความแตกต่างพื้นที่ผิวและปริมาตรของกรวย
“พื้นที่ผิว” คือ ผลรวมของพื้นที่ผิวข้างทุกด้านของรูปทรง
เช่น พื้นที่ผิวของรูปทรงสี่เหลี่ยมมุมฉากจะมีพื้นที่ผิวข้าง 6 ด้านรวมกัน
“ปริมาตร” คือ ปริมาณที่วัดเพื่อแสดงบริเวณที่ว่าง (ความจุ) ภายในรูปทรงสามมิติ
การวัดปริมาตรของรูปทรงสามมิติใช้หน่วยวัดเป็น ลูกบาศก์หน่วย
ปริมาตรกรวย แบบฝึกหัด
1.จงเขียนรูปแสดงความสัมพันธ์ระหว่างทรงกระบอกและกรวย เมื่อทรงกระบอกมีพื้นที่ฐานเท่ากัน
และความสูงเท่ากันกับของกรวย
วิธีทำ
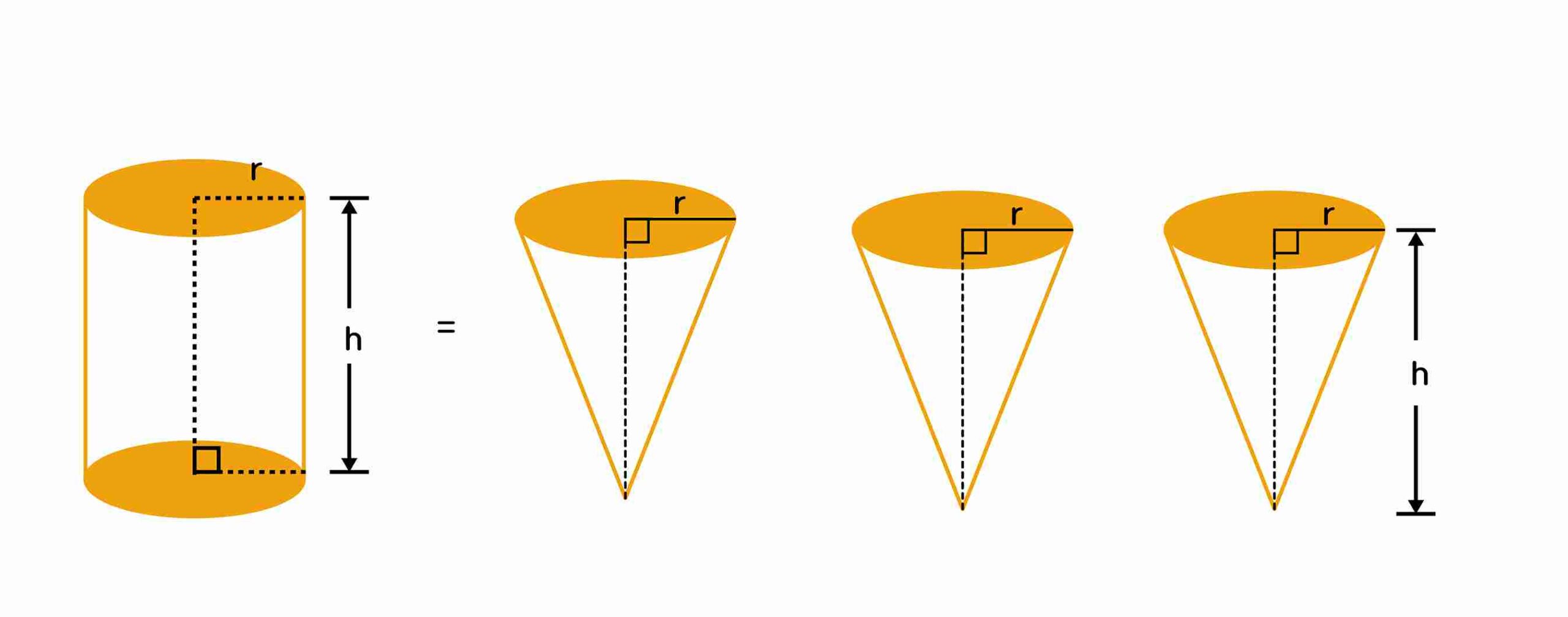
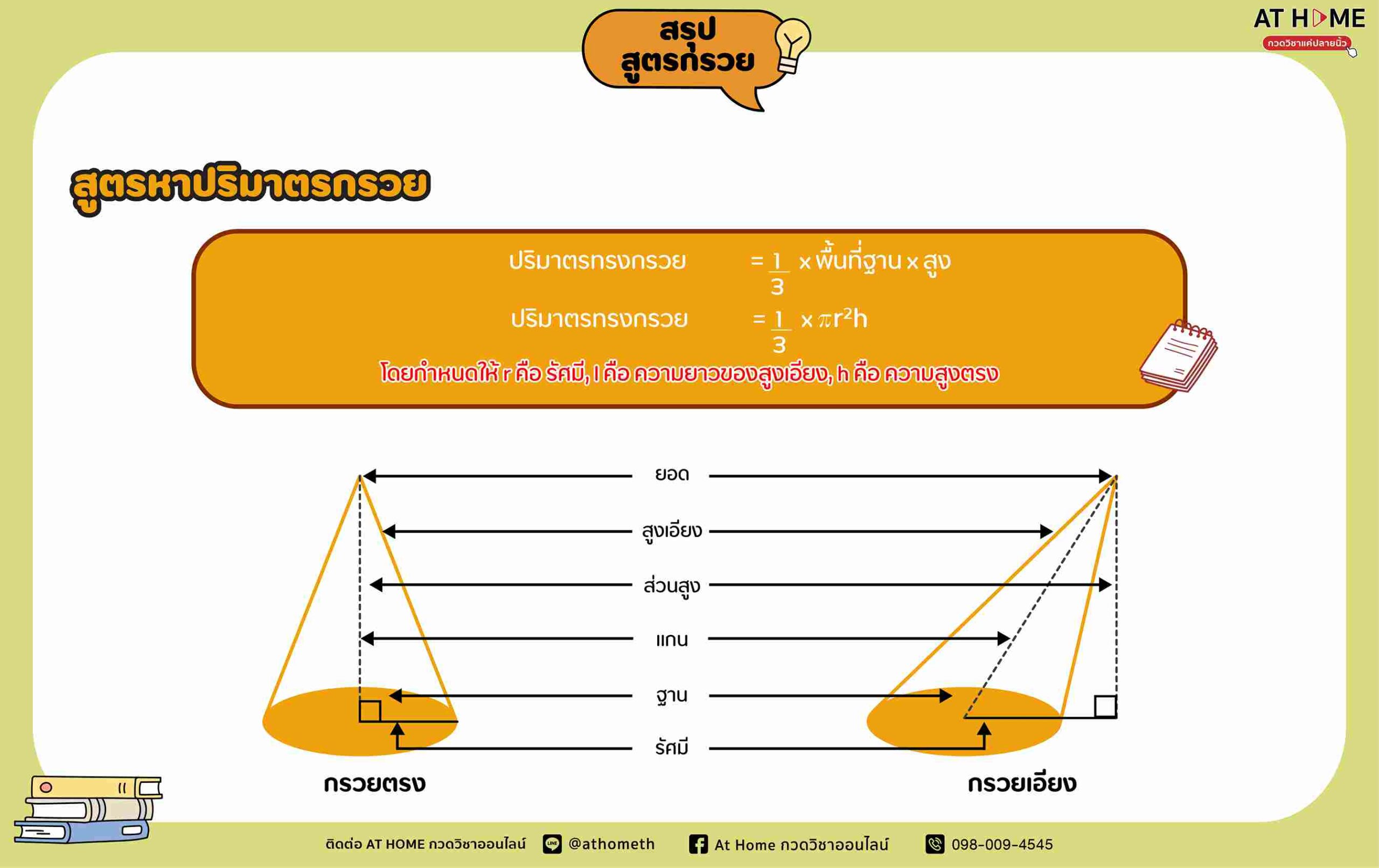
ปริมาตรของกรวย = 1/3 ของปริมาตรของทรงกระบอกที่มีพื้นที่ฐานเท่ากันกับของกรวย และความสูงเท่ากับความสูงของกรวย
ปริมาตรของกรวย = 1/3 x พื้นที่ฐาน x ความสูง
หรือ ปริมาตรของกรวย = 1/3 x r2h ( รอเปลี่ยน root )
2. รูปทรงกรวยดังรูป
จงหา 1. พื้นที่ผิวด้านข้าง 2. พื้นที่ทั้งหมด 3. ปริมาตร
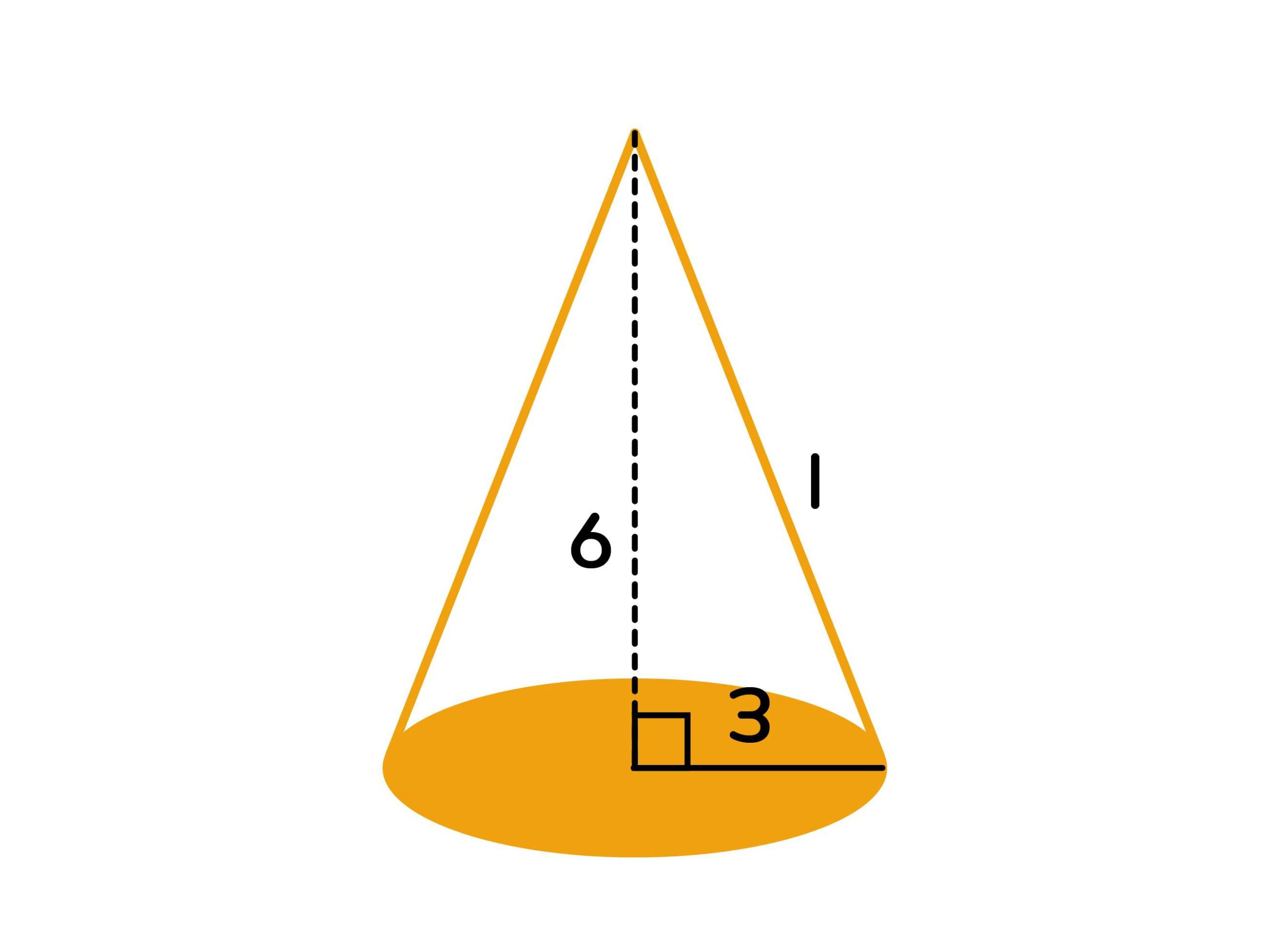
วิธีทำ อันดับแรกให้หาสูงเอียงก่อน แล้วจึงหาสิ่งที่โจทย์ถามต่อไป
ใช้ทฤษฎีบทพีทาโกรัส
l2 = 62 + 32
l2 = 36 + 9 = 45
l = = 3
1. สูตรพื้นที่ผิวด้านข้าง = rl
= (3)( 35) = 95
2. พื้นที่ผิวทั้งหมด = rl + r2
= 95 + (3)2 = 95 + 9 = 9 (5+1)
3. ปริมาตรของทรงกรวย = 1/3 x r2h
= 1/3 ()(3)(3)(6) = 18
( รอเปลี่ยนพายอาร์ / root ทุกบรรทัด ข้อ 1 – 3 )
3. ปริมาตรของรูปนี้ มีค่าเท่ากับเท่าใด
1. 26 ลูกบาศก์หน่วย
2. 26 /2ลูกบาศก์หน่วย
3. 26/3ลูกบาศก์หน่วย
4. 26/5 ลูกบาศก์หน่วย ( รอเปลี่ยนพายอาร์ ข้อ 1 – 4 )
วิธีทำ ใช้รูปสามเหลี่ยมคล้ายเพื่อสร้างสัดส่วน
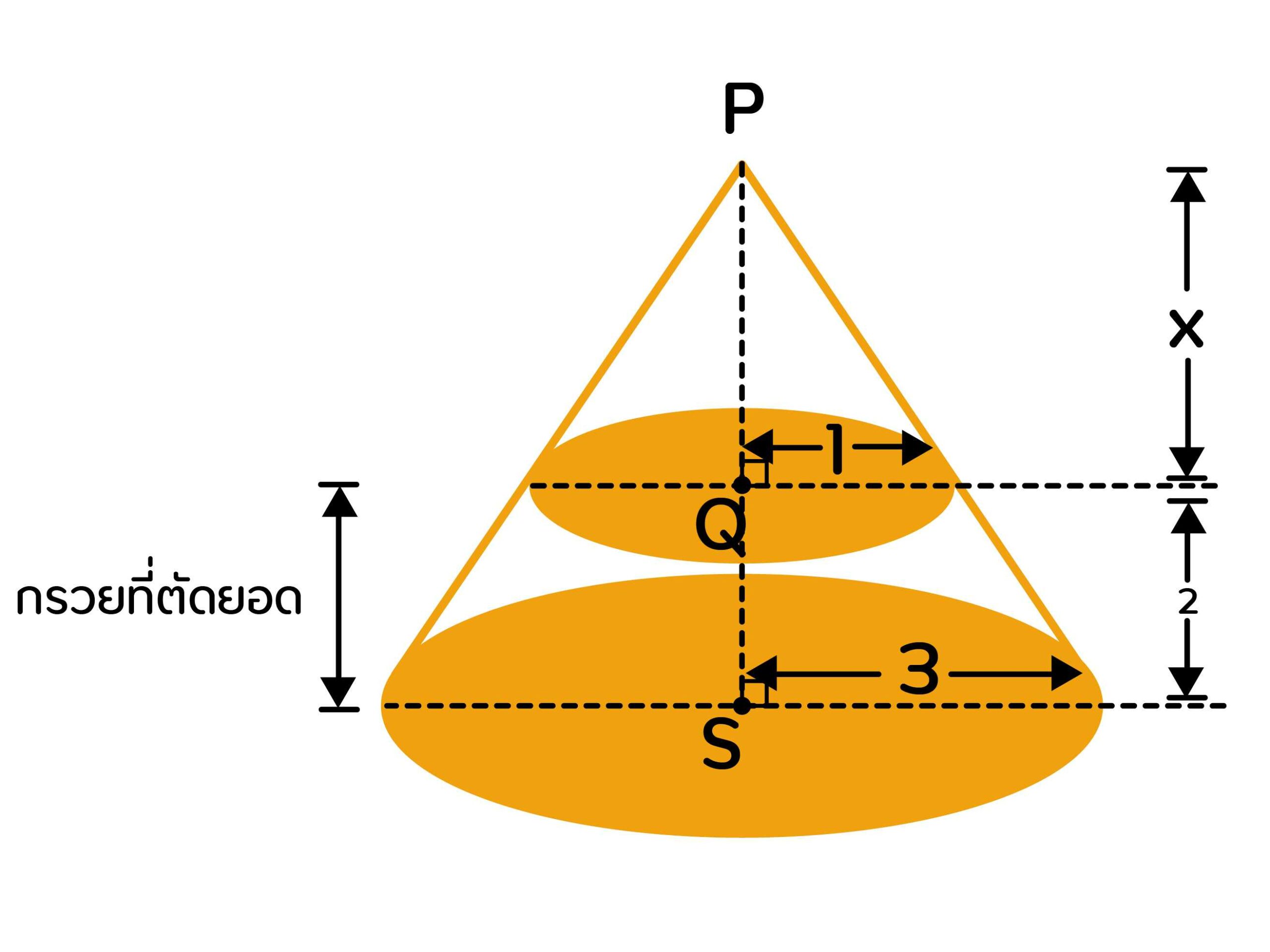
ขั้นตอนที่ 1 หา x
สามเหลี่ยม PQR คล้ายกับ สามเหลี่ยม PST
จะได้
QR/ST = PQ/PS
1/3 = x/x+2
X = 1
สมมติให้
R คือ รัศมีรูปใหญ่ H คือ ความสูงรูปใหญ่
r คือ รัศมีรูปเล็ก h คือ ความสูงรูปเล็ก
ขั้นตอนที่ 2 หาปริมาตรของกรวยที่ตัดยอดออก
ปริมาตรกรวยใหญ่ = ปริมาตรกรวยเล็ก + ปริมาตรกรวยที่ตัดออก
1/3R2 H = 1/3r2 h + ปริมาตรที่โจทย์ถาม
1/3 (3)2 (x+2) = 1/3 (1)2 x + ปริมาตรที่โจทย์ถาม
1/3 (3)2(1+2) = 1/3 (1) + ปริมาตรที่โจทย์ถาม
9 = 1/3 + ปริมาตรที่โจทย์ถาม
ปริมาตรที่โจทย์ถาม = 9 – 1/3
= 26/ 3 ( รอเปลี่ยนพายอาร์ ทุกบรรทัด )
4. จากรูป จงหาปริมาตรของกรวยที่มีหน่วยของความยาวเป็นเซนติเมตร
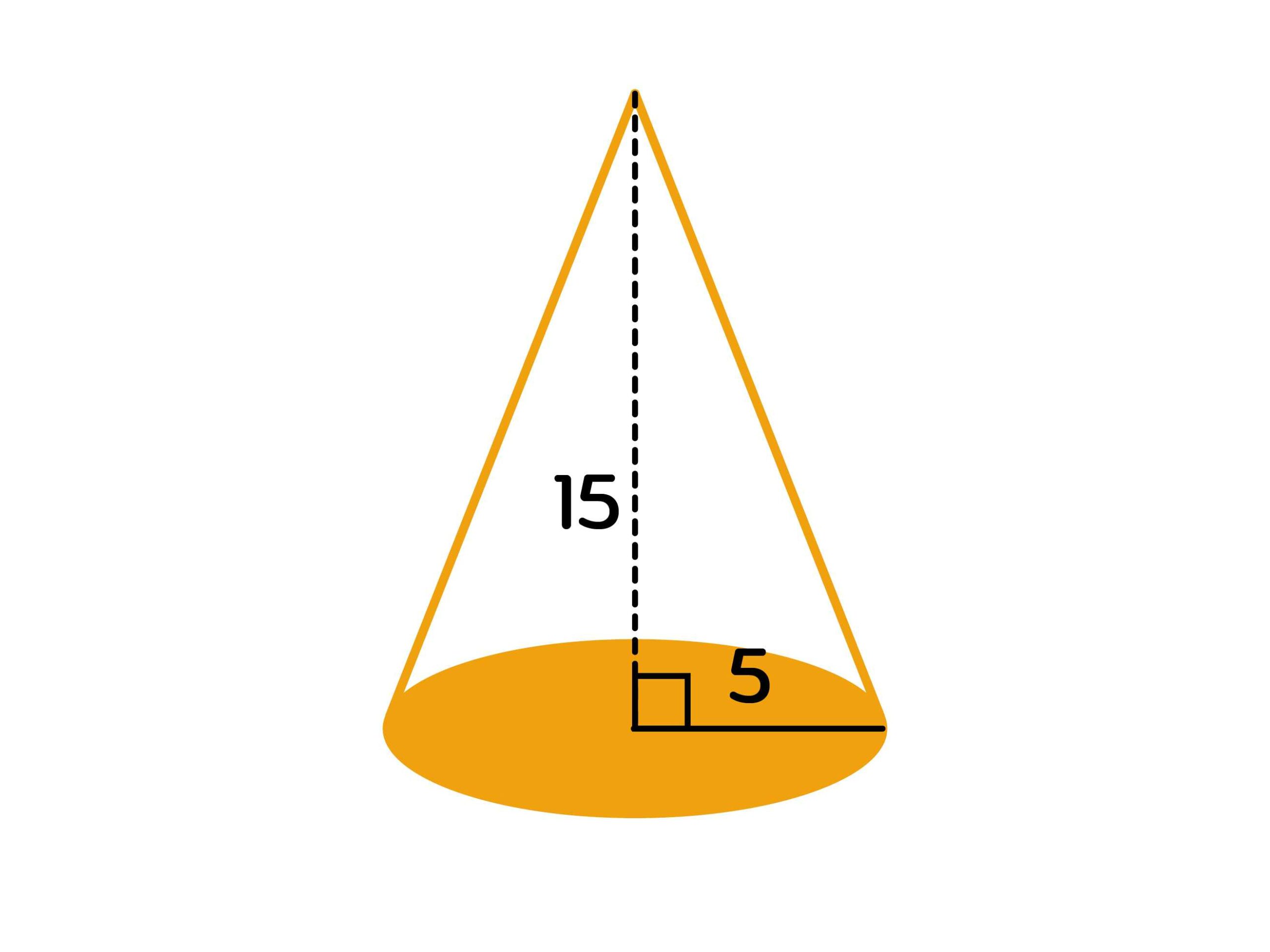
วิธีทำ ปริมาตรของกรวย = 1/3 x พื้นที่ฐาน x สูงตรง
= 1/3 x x 5 x5 x 15
= 125 ลูกบาศก์เซนติเมตร ( รอเปลี่ยนพายอาร์ 2 บรรทัดท้าย )
5. ถ้วยไอศกรีมรูปกรวยสูง 10 เซนติเมตร เส้นผ่านศูนย์กลางภายใน ยาว 6 เซนติเมตร จุไอศกรีมเต็มถ้วยได้ปริมาณเท่าใด
วิธีทำ จากสูตรปริมาตรกรวย = 1/3 x r2 h ( รอเปลี่ยนพายอาร์ )
= 1/3 x 22/7 x 3 x 3 x 10 ( รอเปลี่ยนพายอาร์ )
= 22/7 x 3 x 10
= 660/7
94.29 ลูกบาศก์เซนติเมตร
โจทย์พื้นที่ผิวกรวย พร้อมเฉลย
1. จงหาพื้นที่ผิวของกรวยที่มีรัศมีฐานเท่ากับ 7 เซนติเมตรและความยาวสูงเอียง 15 เซนติเมตร
วิธีทำ เนื่องจากพื้นที่ผิวของกรวย = rl + r2
จะได้ พื้นที่ผิวกรวย = (7)(7) + (7)(15) = 154
= 484 ตารางเซนติเมตร
( รอเปลี่ยนพายอาร์ )
2. จงหาความสูงเอียงของกรวยซึ่งมีพื้นที่ผิวข้าง 50.4 ตารางนิ้ว และรัศมีของฐานกรวยเท่ากับ 1.4 นิ้ว
วิธีทำ เนื่องจาก สูตรพื้นที่ผิวข้าง = rl
จะได้ 50.4 = 22/7 x 1.4 x l
l = 11.45 นิ้ว
( รอเปลี่ยนพายอาร์ )
คำถามที่พบบ่อย (FAQ)
พื้นที่หน้าตัดกรวย หายังไง
หน้าตัดของทรงกรวยคือรูปวงกลม และสูตรหาพื้นที่วงกลม
หาเส้นรอบวงกรวย ยังไง
ความจริงแล้วมีลักษณะมีเป็นโจทย์เหมือนสมการตัวแปรเดียว แต่ใช้หลักการคิดโดยกำหนดตัวแปรที่ต่างกันแทนสองสิ่งที่ต่างกันก่อนแก้สมการ
หาสูงเอียงของกรวย ยังไง
ใช้ทฤษฎีบทพีทาโกรัส
เรื่องกรวยกับการหาพื้นที่หน้าตัด พื้นที่ผิว และปริมาตร เป็นเรื่องที่ต้องอาศัยการจำสูตรในการหาเป็นหลัก รวมถึงการทำความเข้าใจเกี่ยวกับรูปทรงนั้น ๆ ก็สามารถช่วยให้การหาพื้นที่และปริมาตรง่ายขึ้นด้วย สำหรับน้อง ๆ ที่ยังรู้สึกว่าจำสูตรไม่ได้ พี่ ๆ ขอแนะนำให้น้อง ๆ พยายามเลือกโจทย์พื้นฐานมาทำบ่อย ๆ ก่อนเพราะการกระโดดไปทำโจทย์ยาก โจทย์อาจจะไม่ได้โฟกัสเรื่องการใช้สูตรให้เป็น แนะนำให้น้องเลือกโจทย์ง่าย ๆ เพื่อฝึกการแทนค่าและจำการใช้สูตรให้แม่นก่อน แล้วค่อยเพิ่มระดับความยากนะคะ ทำแบบนี้อย่างสม่ำเสมอรับรองว่าคะแนนพุ่งแน่นอน





