“จำนวนจริง” เป็นหนึ่งในโครงสร้างของระบบจำนวนในวิชาคณิตศาสตร์ ในระดับชั้นมัธยมต้น น้องๆจะได้เรียนเฉพาะจำนวนจริงเท่านั้น ยังไม่ได้เรียนไปถึงจำนวนจินตภาพ ซึ่งระบบจำนวนจริงถือเป็นพื้นฐานสำคัญที่เรานำไปประยุกต์ใช้ในบทเรียนอื่นๆได้มากมาย
โครงสร้างของระบบจำนวนเชิงซ้อน
จำนวนและตัวเลขทั้งที่เราได้พบเห็นในชีวิตประจำวันและในบทเรียนต่างๆนั้นมีหลายชนิด
แต่ละชนิดก็มีคุณสมบัติแตกต่างกัน และบางชนิดก็มีความสอดคล้องสัมพันธ์กันอย่างเป็นระบบ
เราสามารถแบ่งชนิดของระบบจำนวนได้ตามโครงสร้างต่อไปนี้
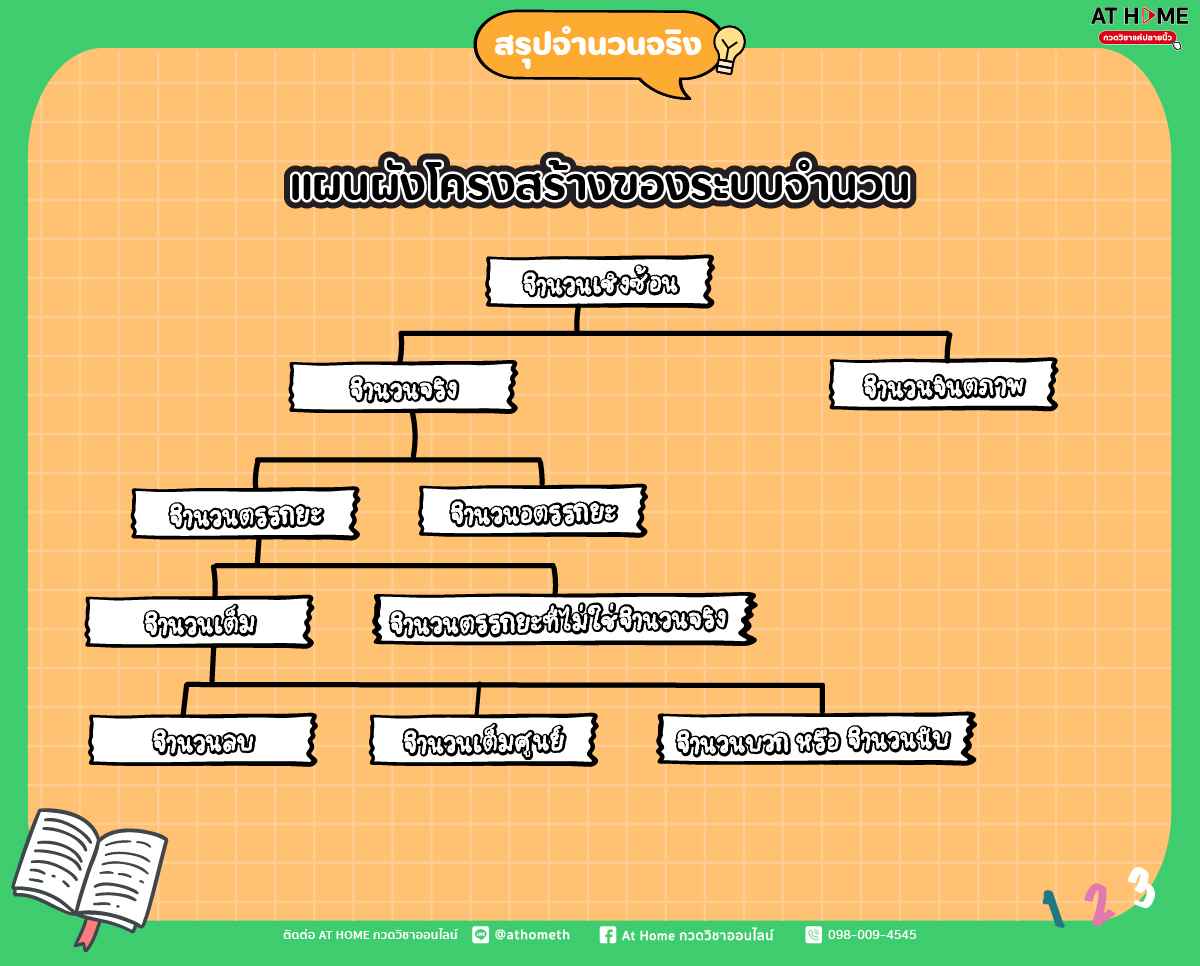
ในระดับมัธยมต้น เราจะยังไม่ได้สนใจจำนวนจินตภาพ แต่จะไปโฟกัสกันที่ระบบจำนวนจริง
ซึ่งโครงสร้างของระบบจำนวนจริง เป็นตามแผนภาพต่อไปนี้
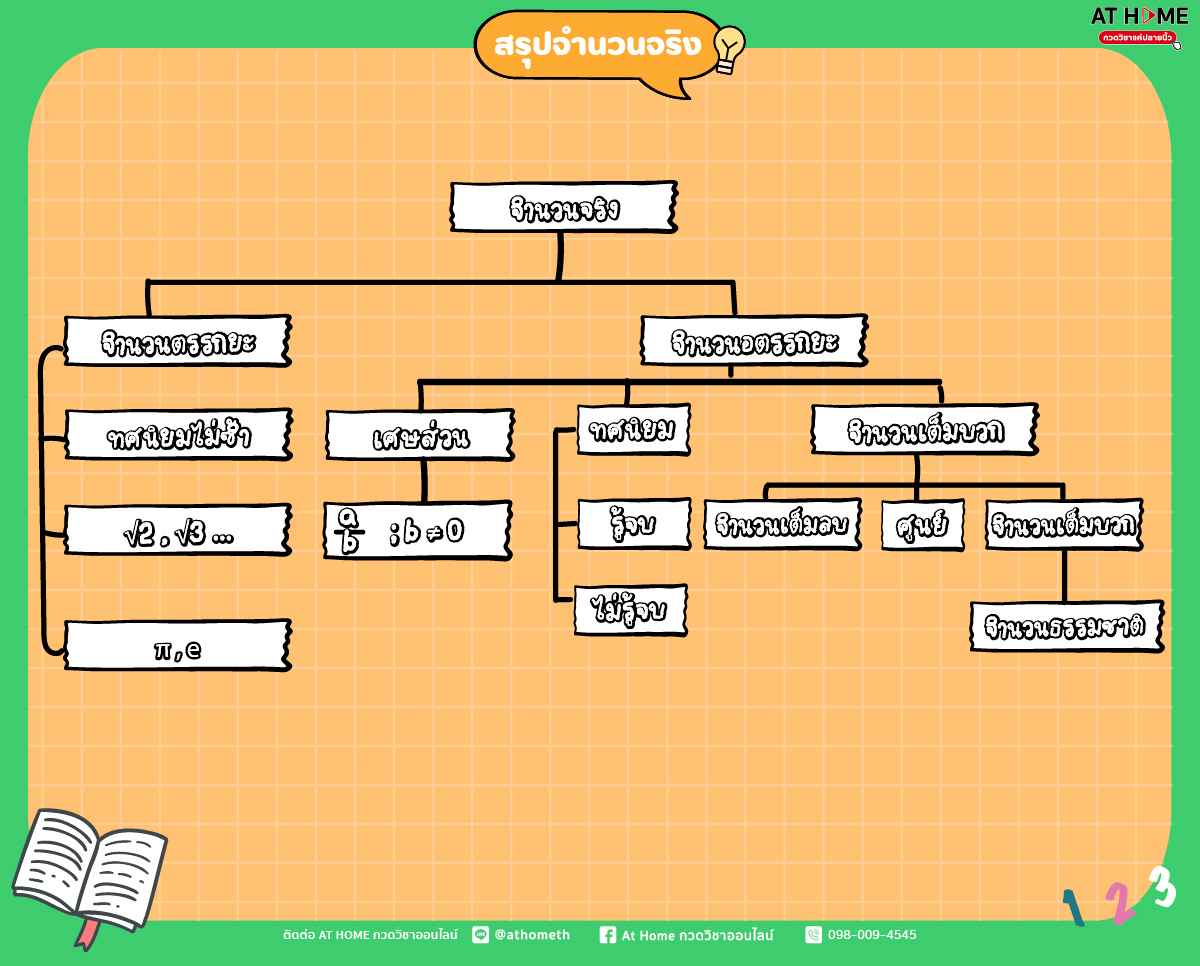
จำนวนจริง
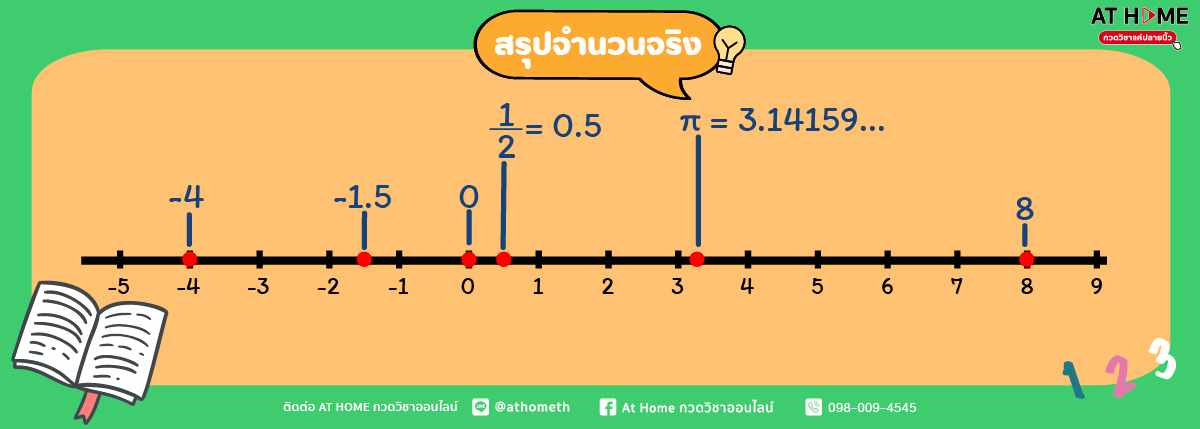
“จำนวนจริง” คือ จำนวนที่มีลักษณะเป็นปริมาณที่สามารถแสดงให้เห็นเป็นภาพโดยใช้จุดบนเส้นจำนวนได้ จำนวนจริงจะประกอบด้วย จำนวนตรรกยะและจำนวนอตรรกยะ เขียนแทนด้วยสัญลักษณ์ ℝ
จำนวนอตรรกยะ
“จำนวนอตรรกยะ” คือ จำนวนที่ไม่สามารถเขียนอยู่ในรูปจำนวนเต็ม เศษส่วนหรือทศนิยมซ้ำได้ เช่น
3.68543800759656…., 2, 3,5 หรือค่า
( รอเปลี่ยนพายอาร์ เเละ root )
จำนวนตรรกยะ
“จำนวนตรรกยะ” คือ จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็มหรือทศนิยมซ้ำได้ ซึ่งแบ่งได้เป็น 2 ประเภท ได้แก่
| 1.จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม เป็นจำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วน (ตัวเศษและตัวส่วนจะต้องเป็นจำนวนเต็มเท่านั้นและไม่เท่ากับ 0) หรือจำนวนที่สามารถเขียนเป็นทศนิยมซ้ำได้ แต่ไม่เต็มจำนวน เช่น 35, -45, 4.38 เป็นต้น |
| 2.จำนวนเต็ม แบ่งได้ 3 ชนิด ได้แก่ – จำนวนเต็มบวก หรือ จำนวนนับ ได้แก่ 1, 2, 3, 4, 5,… – จำนวนเต็มศูนย์ ก็คือ 0 นั่นเอง – จำนวนเต็มลบ ได้แก่ -1, -2, -3, -4,… |
ข้อสังเกตของจำนวนเต็ม
- ไม่มีจำนวนเต็มบวกที่มากที่สุด
- ไม่มีจำนวนเต็มลบที่น้อยที่สุด
- 0 ไม่ใช่ทั้งจำนวนเต็มบวกและจำนวนเต็มลบ
- จำนวนเต็มบวกที่น้อยที่สุด คือ 1
- จำนวนเต็มลบที่มากที่สุด คือ -1
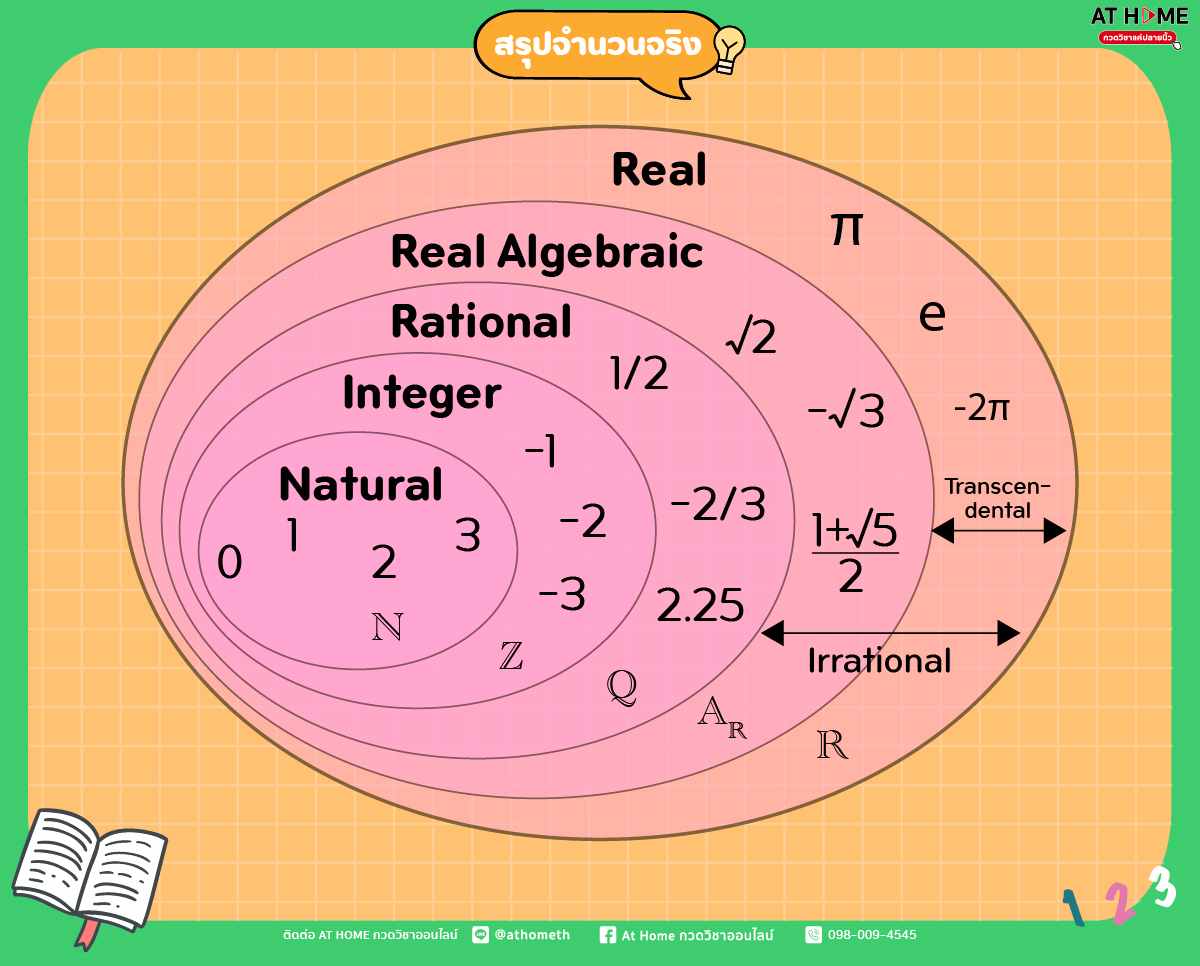
สมบัติของจำนวนจริง
เมื่อกำหนดให้ a, b ,c เป็นจำนวนจริงใดๆ
- สมบัติการสะท้อน a = a
- สมบัติการสมมาตร ถ้า a = b แล้ว b = a
- สมบัติการถ่ายทอด ถ้า a = b และ b = c แล้ว a = c
- สมบัติการบวกด้วยจำนวนที่เท่ากัน
ถ้า a = b แล้ว a + c = b + c
- สมบัติการคูณด้วยจำนวนที่เท่ากัน
ถ้า a = b แล้ว ac = bc
สมบัติการบวกในระบบจำนวนจริง
เมื่อกำหนดให้ a, b ,c เป็นจำนวนจริงใดๆ
- สมบัติปิดการบวก a + b จะได้ผลลัพธ์เป็นจำนวนจริง
- สมบัติการสลับที่ของการบวก a + b = b + c
- สมบัติการเปลี่ยนกลุ่มการบวก a + (b + c) = (a + b) + c
- เอกลักษณ์การบวก
0 + a = a = a + 0 เพราะฉะนั้นในระบบจำนวนจริงจะมี 0 เป็นเอกลักษณ์การบวก
- อินเวอร์สการบวก
a + (-a) = 0 = (-a) + a เพราะฉะนั้นในระบบจำนวนจริง จำนวน a จะมี -a เป็นอินเวอร์สของการบวก
สมบัติการคูณในระบบจำนวนจริง

ทฤษฎีบทของระบบจำนวนจริง

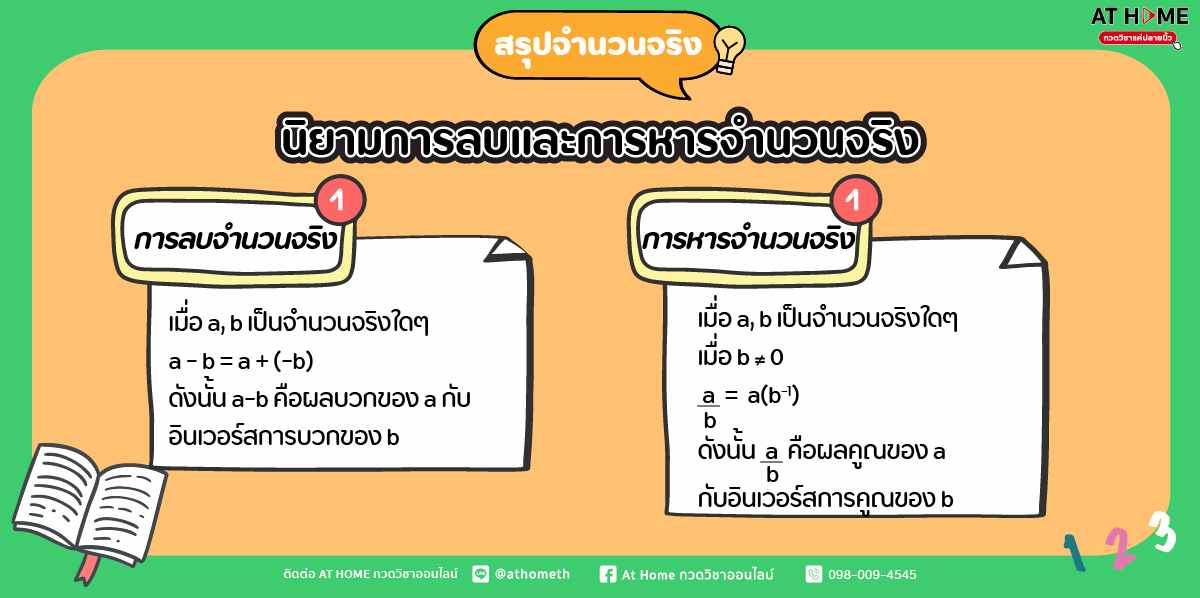
นิยามการลบและการหารจำนวนจริง
สรุปจำนวนจริงคืออะไร ประกอบด้วยอะไรบ้าง
และยกตัวอย่างจำนวนจริง
“จำนวนจริง” คือ จำนวนที่มีลักษณะเป็นปริมาณที่สามารถแสดงให้เห็นเป็นภาพโดยใช้จุดบนเส้นจำนวนได้ จำนวนจริงจะประกอบด้วย จำนวนตรรกยะและจำนวนอตรรกยะ เขียนแทนด้วยสัญลักษณ์ ℝ
ตัวอย่างจำนวนจริง








