เส้นขนาน และ มุมภายใน เป็นเนื้อหาคณิตศาสตร์ระดับม.ต้นที่สามารถนำไปประยุกต์ได้มากกับบทเรขาคณิตต่าง ๆ ไม่ว่าจะเป็นเรื่องวงกลม หรือรูปเรขาคณิตต่า ๆ อีกมากมาย เป็นบทพื้นฐานที่จะทำให้เข้าใจเรื่องเรขาคณิตได้ดียิ่งขึ้น นอกจากนี้บทนี้ยังเป็นบทเริ่มต้นที่จะปูเนื้อหาไปยังเรื่องคุณสมบัติต่าง ๆ ของรูปสามเหลี่ยมอีกด้วย
เส้นขนาน คือ

บทนิยาม เส้นขนาน คืออะไร
บทนิยาม เส้นขนาน คือ เส้นตรงสองเส้นที่อยู่บนระนาบเดียวกัน
ขนานกันก็ต่อเมื่อ เส้นตรงสองเส้นนั้นไม่ตัดกัน
สมบัติของเส้นขนาน
| เส้นตรงสองเส้นที่อยู่บนระนาบเดียวกัน |
| ถ้าเส้นตรงสองเส้นขนานกัน แล้วระยะห่างระหว่างเส้นตรงคู่นั้น จะเท่ากันเสมอ และในทางกลับกัน ถ้าเส้นตรงสองเส้นมีระยะห่าง ระหว่างเส้นตรงเท่ากันเสมอ แล้วเส้นตรงคู่นั้นจะขนานกัน |
| เส้นตรงสองเส้นที่กำ หนดให้จะขนานกันหรือไม่ สามารถตรวจสอบ จากระยะห่างระหว่างเส้นตรงทั้งสองที่วัดจากจุดที่แตกต่างกัน อย่างน้อยสองจุด หรือพิจารณาจากขนาดของมุมภายในที่อยู่บน ข้างเดียวกันของเส้นตัด ขนาดของมุมแย้ง หรือขนาดของ มุมภายนอกและมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของเส้นตัด |
| ถ้าต่อด้านใดด้านหนึ่งของรูปสามเหลี่ยมออกไป แล้วมุมภายนอก ที่เกิดขึ้นจะมีขนาดเท่ากับผลบวกของขนาดของมุมภายในที่ไม่ใช่ มุมประชิดของมุมภายนอกนั้น |
ระยะห่างระหว่างเส้นขนาน
ในกรณที่ เส้นตรง AB ขนานกับ เส้นตรง CD จะได้ว่า EF = XY นั่นคือระยะห่างระหว่างเส้นตรง AB
และเส้นตรง CD ที่วัดจากจุดที่แตกต่างกันบนเส้นตรง AB จะเท่ากันเสมอ
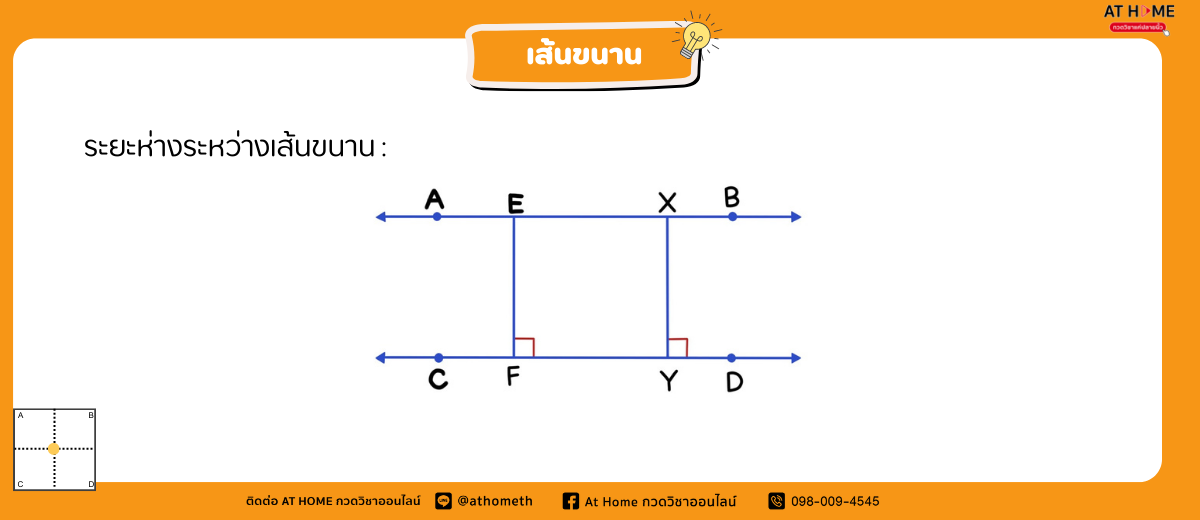
ในกรณีทั่วไป ถ้าเส้นตรงสองเส้นขนานกัน ระยะห่างระหว่างเส้นตรงสองเส้นนั้นจะเท่ากันเสมอ และในทางกลับกัน ถ้าเส้นตรงทั้งสองเส้นมีระยห่างเท่ากันเสมอ แล้วเส้นตรงคู่นั้นจะขนานกัน
เส้นขนานและมุมภายใน
ในการตรวจสอบว่าเส้นใดเป็นเส้นขนานด้วยการวัดระยะห่างของเส้นขนานแล้วนั้น ยังสามารถพิจารณามุมภายในที่มุมข้างเดียวกันของเส้นตัด ดังต่อไปนี้
ตัวอย่าง
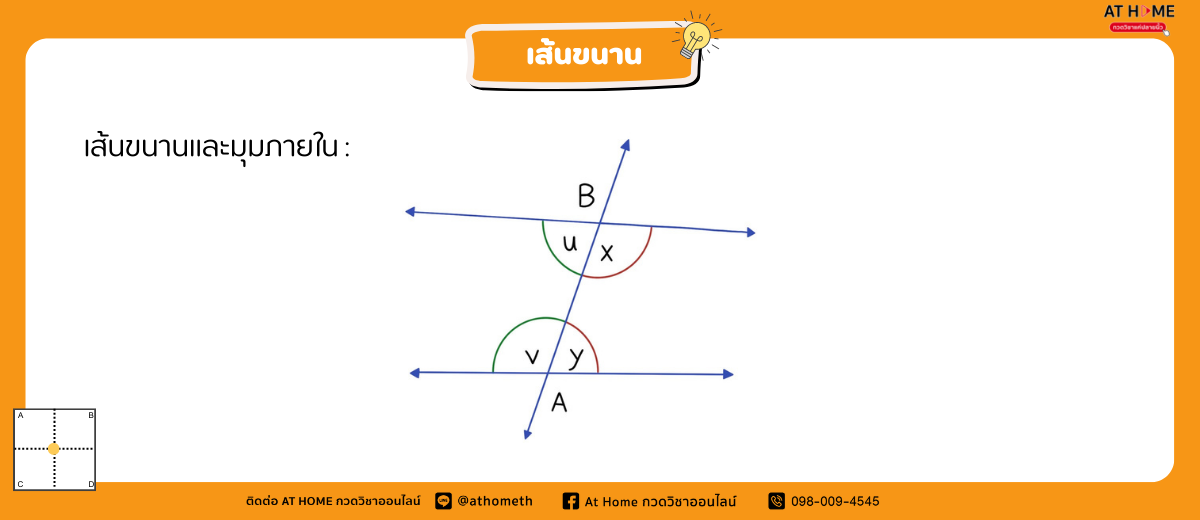
จากรูป เส้นตรง AB เรียกว่า เส้นตัด AB
เรียกมุม x และ มุม y ว่า มุมภายในที่อยู่บนข้างเดียวกันกับเส้นตัด AB
และ เรียกมุม u และ มุม v ว่า มุมภายในที่อยู่บนข้างเดียวกันของเส้นตัด AB ด้วย
สมบัติของเส้นขนานกับมุมภายใน
- ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัด แล้วขนาดมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดรวมกันเท่ากับ 180 องศา
- ถ้าเส้นตรงเส้นหนึ่งตัดกับเส้นตรงคู่หนึ่ง ทำให้ขนาดของมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดรวมกันเท่ากับ 180 องศา แล้วเส้นตรงคู่นั้นจะขนานกัน
แบบฝึกหัด เรื่อง เส้นขนานและมุมภายใน
วิธีทำ เนื่องจาก เส้นตรง PQ // เส้นตรง RS และมี เส้นตรง AB เป็นเส้นตัด ทำ ให้มุมภายนอกและมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของ เส้นตัดมีขนาดเท่ากัน
จะได้ มุม APQ = มุม ARS และ มุม BRS = มุม BPQ
วิธีทำ เนื่องจาก เส้นตรง MN // เส้นตรง KL และมี เส้นตรง เส้นตรง PQ เป็นเส้นตัด
ทำให้มุมภายนอกและมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของ เส้นตัดมีขนาดเท่ากัน
จะได้ มุม NST = มุม LTP
เนื่องจาก เส้นตรง MN // เส้นตรง KL และมี เส้นตรง PQ เป็นเส้นตัด ทำ ให้มุมแย้งมีขนาดเท่ากัน
จะได้ มุม NST = มุม STK
เนื่องจาก เส้นตรง MN ตัดกับ เส้นตรง PQ
ทำ ให้มุมตรงข้ามมีขนาดเท่ากัน
จะได้ มุม NST = มุม QSM
ดังนั้น มุม NST = มุม LTP = มุม STK = มุม QSM
วิธีทำ ลาก เส้นตรง EH ขนานกับ เส้นตรง AB จะได้ เส้นตรง EH // เส้นตรง CD ด้วย
(สมบัติถ่ายทอดของการขนาน) เนื่องจาก เส้นตรง AB // เส้นตรง EH และมี เส้นตรง EF เป็นเส้นตัด
จะได้ มุม AEH = 52° (ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัด แล้วมุมภายนอกและ มุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของเส้นตัดมีขนาดเท่ากัน)
เนื่องจาก มุม AEC = 104° (กำหนดให้)
จะได้ มุม HEC = 104 – 52 = 52° (สมบัติของการเท่ากัน)
เนื่องจาก เส้นตรง EH // เส้นตรง CD และมี เส้นตรง EC เป็นเส้นตัด
จะได้ มุม HEC + มุม ECD = 180°
(ขนาดของมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดที่ตัดเส้นขนาน รวมกันเท่ากับ 180°)
ดังนั้น มุม ECD = 180 – 52 = 128° (สมบัติของการเท่ากัน)
เส้นขนานและมุมแย้ง
พิจารณารูปต่อไปนี้
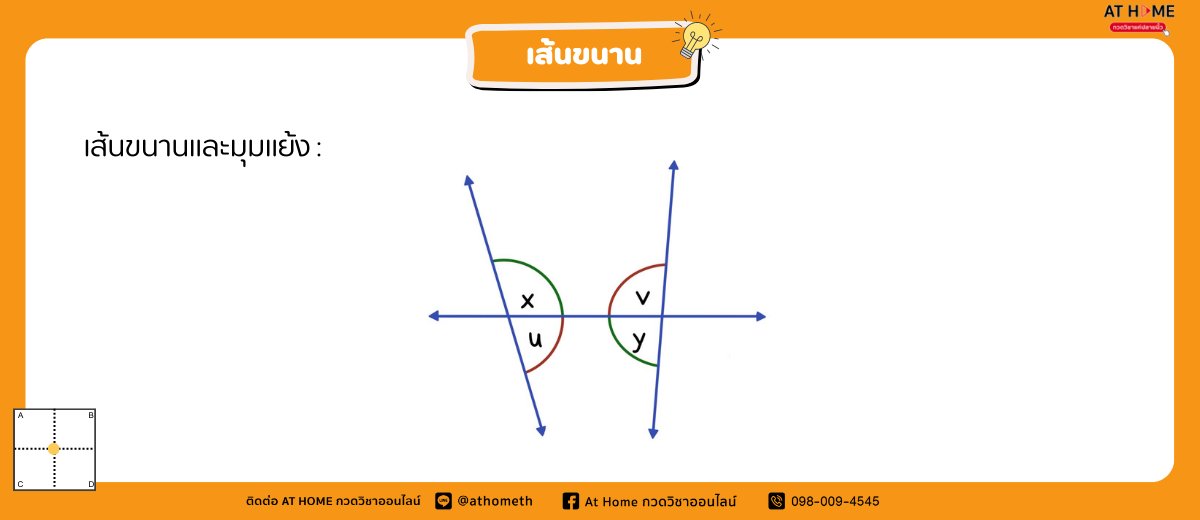
จากรูป มุม x และ มุม y เป็นมุมแย้ง และ เรียก มุม u และมุม v ว่าเป็นมุมแย้ง
ทฤษฎีบท ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัด แล้วมุมแย้งจะมีขนาดเท่ากัน
ตัวอย่าง
- กำหนดให้ AB // CD และมี XY เป็นเส้นตัด ดังรูป จงอธิบายว่ามุมใดมีขนาดเท่ากันบ้าง
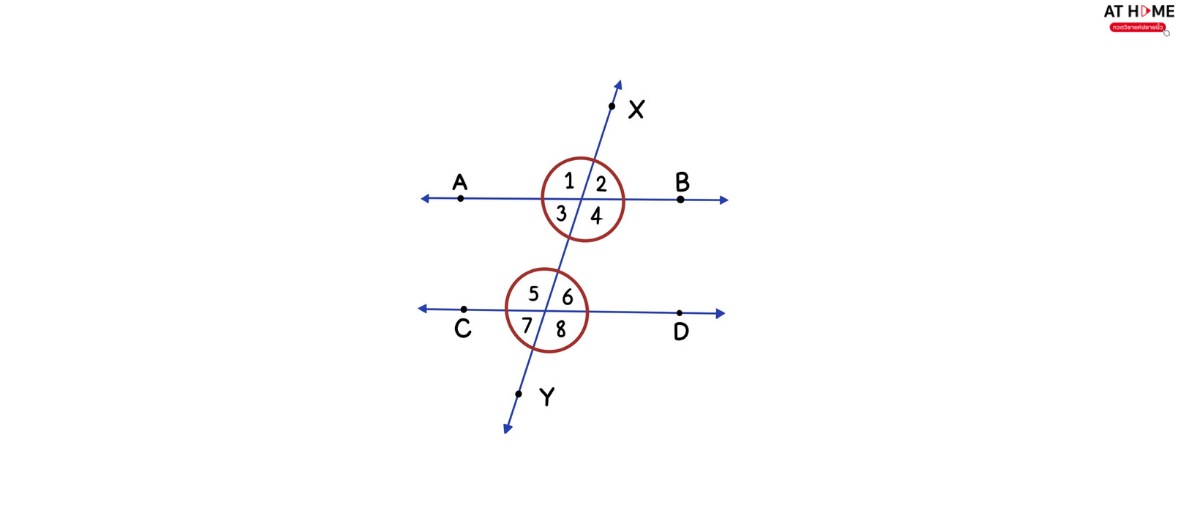
วิธีทำ เนื่องจาก AB // CD มี XY เป็นเส้นตัด จะได้มุมแย้งเท่ากันคือ
3 = 6 และ 4 = 5
เนื่องจาก XY ตัดกับ AB และ CD จะได้มุมตรงข้ามขนาดเท่ากันคือ
1 = 4 2 = 3 5 = 8 6 = 7
จากสมบัติการเท่ากัน จะได้ว่า
1 = 4 = 5 = 8
2 = 3 = 6 = 7
เส้นขนานกับมุมภายนอกและมุมภายใน
พิจารณารูปต่อไปนี้
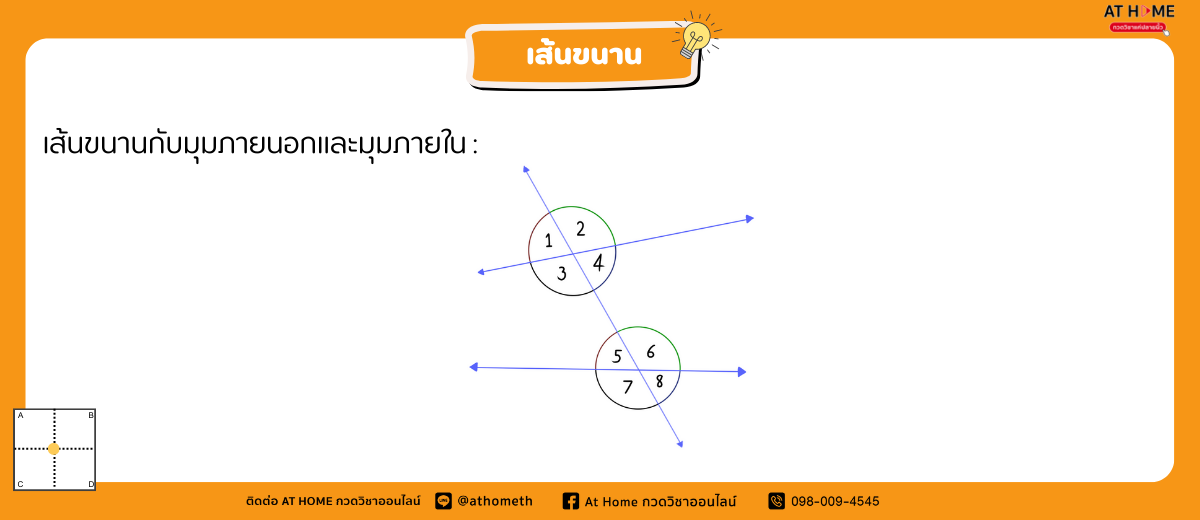
เรียก มุม 1 , 2 , 7 , 8 ว่า มุมภายนอก
เรียกมุม 3, 4 , 5 , 6 ว่า มุมภายใน
เรียกมุม 1, 5 ว่า มุมภายนอกและมุมภายใน ที่อยู่ตรงข้ามของข้างเดียวกันของเส้นตัด
ในทำนองเดียวกัน จะเรียกมุม 2 และมุม 6 , 7 , 3 , 8 , 4 แต่ละคู่ว่าเป็น มุมภายนอกและมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของเส้นตัด
ทฤษฎีบท
ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัด แล้วมุมภายนอก และมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกัน
ของเส้นตัดมีขนาดเท่ากัน
เส้นขนานกับรูปสามเหลี่ยม
ทฤษฎีบท ขนาดของมุมภายในทั้งสามมุมของรูปสามเหลี่ยมรวมกันเท่ากับ 180 องศา
ทฤษฎีบทข้างต้น สามารถนำมาใช้พิสูจน์ทฤษฎีบทเกี่ยวกับขนาดของมุมภายนอกและขนาดของมุมภายในของรูปสามเหลี่ยมได้ดังต่อไปนี้
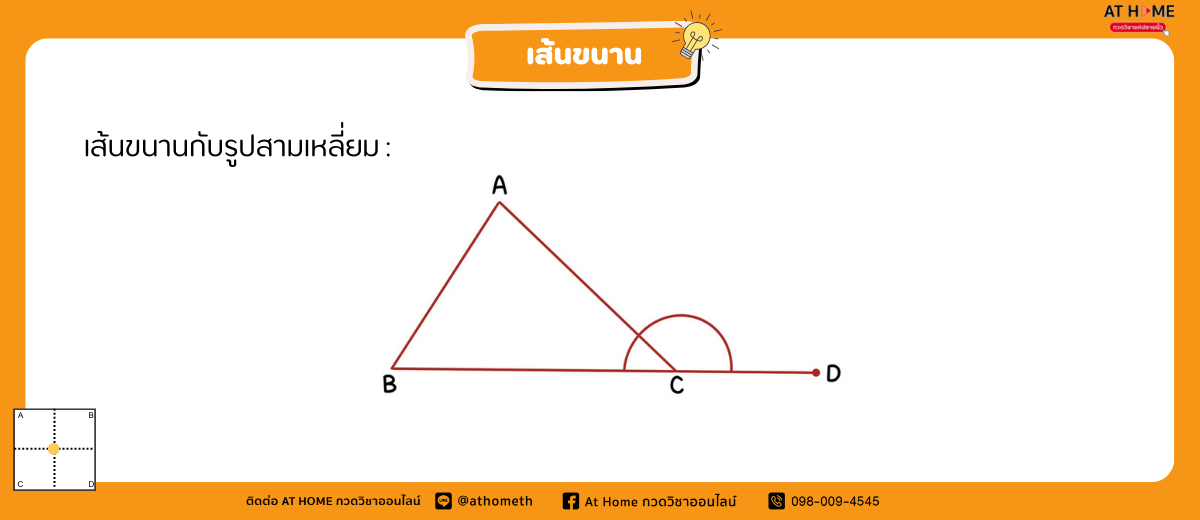
จากรูป กำหนดสามเหลี่ยม ABC และต่อเส้นตรง BC ออกไปทางจุด C ถึงจุด D เรียกว่ามุม ACD ว่ามุมภายนอกของสามเหลี่ยม ABC เรียก มุม ACB และ มุม ACD ว่าเป็นมุมประชิด หรืออาจเรียกว่า มุม ACB เป็นมุมประชิดของ มุม ACD
ทฤษฎีบท
ถ้าต่อด้านใดด้านหนึ่งของรูปสามเหลี่ยมออกไป มุมภายนอกที่เกิดขึ้นจะมีขนาดเท่ากับผลบวกของขนาดของมุมภายในที่ไม่ใช่มุมประชิดของมุมภายนอกนั้น นอกจากทฤษฎีบทดังกล่าวแล้ว ยังมีการนำทฤษฎีบทเกี่ยวกับผลบวกของขนาดของมุมภายในของรูปสามเหลี่ยม ไปพิสูจน์สมบัติที่เกี่ยวกับความเท่ากันทุกประการของรูปสามเหลี่ยมดังต่อไปนี้
ทฤษฎีบท
ถ้ารูปสามเหลี่ยมสองรูปมีมุมที่มีขนาดเท่ากันสองคู่ และด้านคู่ที่อยู่ตรงข้ามกับมุมคู่ที่มีขนาดเท่ากัน ยาวเท่ากันหนึ่งคู่แล้วรูปสามเหลี่ยมสองรูปนั้นเท่ากันทุกประการ
แบบฝึกหัด เรื่อง เส้นขนานและรูปสามเหลี่ยม
วิธีทำ เนื่องจาก เส้นตรง BA // เส้นตรง CE และมี เส้นตรง BC เป็นเส้นตัด
จะได้ 64 + (x + 68) = 180
(ขนาดของมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดที่ตัดเส้นขนาน รวมกันเท่ากับ 180°)
ดังนั้น x = 48 (สมบัติของการเท่ากัน)
วิธีทำ เนื่องจาก มุม ABE = มุม BCF = 128° (กำหนดให้)
จะได้ เส้นตรง BE // เส้นตรง CF
(ถ้าเส้นตรงเส้นหนึ่งตัดเส้นตรงคู่หนึ่ง ทำ ให้มุมภายนอกและ มุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของเส้นตัดมีขนาดเท่ากัน แล้วเส้นตรงคู่นั้นขนานกัน)
เนื่องจาก มุม CEF = 81° (กำหนดให้)
จะได้ มุม CFE + 46 + 81 = 180 (ขนาดของมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดที่ตัด เส้นขนานรวมกันเท่ากับ 180°)
ดังนั้น มุม CFE = 53° (สมบัติของการเท่ากัน)
วิธีทำ พิจารณา ∆CDE
จะได้ 106 = y + 90
(ขนาดของมุมภายนอกของรูปสามเหลี่ยมเท่ากับผลบวกของขนาดของมุมภายในที่ไม่ใช่มุมประชิดของมุมภายนอกนั้น)
ดังนั้น y = 16 (สมบัติของการเท่ากัน)
จะได้ มุม ACD = 90 – y = 90 – 16 = 74° (สมบัติของการเท่ากัน)
จะได้ x = 74 (ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัด แล้วมุมแย้งมีขนาดเท่ากัน)
ดังนั้น x + y = 74 + 16 = 78
วิธีทำ เนื่องจาก มุม DAE + 130 = 180 (ขนาดของมุมตรง)
จะได้ มุม DAE = 50° (สมบัติของการเท่ากัน)
พิจารณา ∆ABC
จะได้ 120 = y + 50 (ขนาดของมุมภายนอกของรูปสามเหลี่ยมเท่ากับผลบวกของขนาดของมุมภายในที่ไม่ใช่มุมประชิดของมุมภายนอกนั้น)
ดังนั้น y = 70 (สมบัติของการเท่ากัน)
เนื่องจาก มุม ADE = 100° (ถ้าเส้นตรงสองเส้นตัดกัน แล้วมุมตรงข้ามมีขนาดเท่ากัน)
พิจารณา ∆ADE
จะได้ x = 100 + 50 = 150 (ขนาดของมุมภายนอกของรูปสามเหลี่ยมเท่ากับผลบวกของขนาดของมุมภายในที่ไม่ใช่มุมประชิดของมุมภายนอกนั้น)
วิธีทำ เนื่องจาก เส้นตรง DG // เส้นตรง AC และมี EC เป็นเส้นตัด (กำหนดให้)
จะได้ x = 54 (ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัด
แล้วมุมภายนอกและมุมภายในที่อยู่ตรงข้ามบน ข้างเดียวกันของเส้นตัดมีขนาดเท่ากัน)
เนื่องจาก มุม ABD = มุม FBG = 48° (ถ้าเส้นตรงสองเส้นตัดกัน แล้วมุมตรงข้ามมีขนาดเท่ากัน)
และ 54 + 48 + y = 180 (ขนาดของมุมตรง)
จะได้ y = 78 (สมบัติของการเท่ากัน)
ดังนั้น (x – y)2 = (54 – 78)2 = 576
วิธีทำ เนื่องจาก ∆EAB เป็นรูปสามเหลี่ยมหน้าจั่ว
จะได้ มุม 1 = มุม 2 (มุมที่ฐานของรูปสามเหลี่ยมหน้าจั่วมีขนาดเท่ากัน)
เนื่องจาก เส้นตรง XY // เส้นตรง AB มี เส้นตรง AE เป็นเส้นตัด (กำหนดให้)
จะได้ มุม 1 = มุม 3 และ มุม 2 =มุม 5
(ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัด แล้วมุมแย้ง มีขนาดเท่ากัน)
และ มุม 1 = มุม 4 และ มุม 2 = มุม 6 (ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัด แล้วมุมภายนอก และมุมภายในที่อยู่ตรงข้ามบนข้างเดียวกันของเส้นตัดมีขนาด เท่ากัน)
ดังนั้น มุม 1 = มุม 2 = มุม 3 = มุม 4 = มุม 5 = มุม 6
แบบฝึกหัด เส้นขนาน และมุมแย้ง
จากรูป กำ หนดให้ เส้นตรง PQ // เส้นตรง RS, เส้นตรง RS // เส้นตรง MN และ เส้นตรง TR // เส้นตรง MQ จงหาค่าของ x + y + z
วิธีทำ
เนื่องจาก มุม RSQ และ มุม PQS เป็นมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดที่ตัดเส้นขนาน
จะได้ มุม RSQ = 180 – 55 = 125° เนื่องจาก ขนาดของมุมภายนอกของรูปสามเหลี่ยมเท่ากับผลบวกของขนาดของมุมภายในที่ไม่ใช่มุมประชิดของ มุมภายนอกนั้น จะได้ มุม RSQ = y + z
ดังนั้น y + z = 125 เนื่องจาก เส้นตรง TR // เส้นตรง MQ และมี เส้นตรง RS เป็นเส้นตัด จะได้ x = 125
ดังนั้น x + y + z = 125 + 125 = 250
จากรูป กำ หนดให้ เส้นตรง AB // เส้นตรง DF และ เส้นตรง AC // เส้นตรง DE
จงหาค่าของ a และ b
วิธีทำ ลาก เส้นตรง CG // เส้นตรง DF
ดังนั้น เส้นตรง CG // เส้นตรง AB ด้วย เนื่องจาก มุม BAC และ มุม ACG เป็นมุมภายในที่อยู่บนข้างเดียวกัน ของเส้นตัดที่ตัดเส้นขนาน
จะได้ มุม ACG = 180 – 150 = 30° ดังนั้น มุม GCD = 80 – 30 = 50° เนื่องจาก มุม GCD และ มุม CDF เป็นมุมภายในที่อยู่บนข้างเดียวกัน ของเส้นตัดที่ตัดเส้นขนาน จะได้ มุม CDF = 180 – 50 = 130°
ดังนั้น a = 130
- กำหนดให้ เส้นตรง AC // เส้นตรง DE, มุม BAC = 114° และ มุม ABC = 38° จงหาขนาดของ มุม CDE พร้อมแสดงเหตุผล
วิธีทำ เนื่องจาก มุม BAC = 114° และ มุม ABC = 38°
พิจารณา ∆ABC
เนื่องจาก มุม ACB + 114 + 38 = 180°
(ขนาดของมุมภายในทั้งสามมุมของรูปสามเหลี่ยมรวมกันเท่ากับ 180° )
จะได้ มุม ACB = 28° (สมบัติของการเท่ากัน)
เนื่องจาก เส้นตรง AC // เส้นตรง DE และมี เส้นตรง CD เป็นเส้นตัด
ดังนั้น มุม CDE = 28° (ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัดแล้วมุมแย้งมีขนาดเท่ากัน)
คำถามที่พบบ่อย (FAQ)
มุมแย้ง คือ
มุมที่เกิดจากเส้นตรงเส้นหนึ่งตัดเส้นขนานคู่หนึ่ง อยู่เยื้องกันคนละข้างของเส้นตัด ภายในเส้นขนานคู่นั้น มุม 2 มุมบนเส้นตรงเดียวกันรวมกันได้ 180 องศา หรือ 2 มุมฉาก
มุมตรงข้าม คือ
มุม 2 มุมที่มีขนาดเท่ากัน และเกิดจากเส้นตรง 2 เส้นตัดกันดังรูป a เป็นมุมตรงข้ามกับ a´ หรือ กลับกัน b เป็นมุมตรงข้ามกับ b´หรือ กลับกัน
มุมภายใน คือ
มุมที่เกิดจากด้านสองด้านที่มีจุดปลายข้างหนึ่งร่วมกัน ภายในรูปหลายเหลี่ยมเชิงเดียว ซึ่งรูปหลายเหลี่ยมเชิงเดียวนี้จะมีมุมภายในหนึ่งมุมต่อหนึ่งจุดยอด
เป็นอย่างไรบ้างคะน้อง ๆ พอจะเข้าใจเกี่ยวกับเส้นขนานมากขึ้นแล้วใช่ไหมคะ บทเรียนนี้ไม่ได้เป็นบทที่เน้นไปที่การจำสูตร แต่เน้นไปที่ความเข้าใจเกี่ยวกับบทนิยามมากกว่า หากน้อง ๆ สามารถทำความเข้าใจว่ามุมภายในและมุมภายนอกเกี่ยวข้องกับเส้นขนานอย่างไร ก็จะทำให้น้อง ๆ สามารถหาค่าตัวแปรซึ่งแทนเป็นมุมต่าง ๆ ในโจทย์ได้ดีมากขึ้น หากอยากได้คะแนนบทนี้สูง ๆ พี่ ๆ ขอแนะนำให้น้อง ๆ หมั่นทำโจทย์ที่มีความซับซ้อนของรูปแบบบ่อย ๆ มากขึ้น จะช่วยให้จำทฤษฎีบทได้ดีขึ้นนะคะ





