สรุปพื้นฐาน “พาราโบลา” เบื้องต้นฉบับเข้าใจง่าย

เริ่มออกสตาร์ทเปิดเทอมกันมาพักใหญ่แล้วสำหรับเด็กมัธยมต้น บทเรียนใหม่ๆน่าสนุกกำลังรอน้องๆอยู่ โดยเฉพาะน้องม.3 ที่จะได้เจอกับบทเรียนคณิตศาสตร์ชื่อแปลกอย่าง “พาราโบลา” ที่ดูเหมือนจะยาก แต่บอกเลยว่าง่ายนิดเดียว เพราะพี่ๆ AT HOME สรุปมาให้ครบแบบเข้าใจง่าย ตั้งแต่พาราโบลาคืออะไร ภาคตัดกรวย จุดยอด จุดกำเนิดเป็นแบบไหน รวมไปถึงสูตรพาราโบลาที่จำเป็นต้องรู้! ปิดท้ายด้วยแบบฝึกหัดเสริมประสบการณ์ให้ลองได้ทำกัน แต่ถ้าใครอยากพื้นฐานแน่นแบบเน้นๆ ขอบอกว่าคอร์สเรียนเรื่อง “พาราโบลา”ของอาจารย์รี่นั้น เจาะลึกและตอบทุกข้อสงสัยของทุกคนได้อย่างแน่นอน

พาราโบลาคืออะไร 

‘พาราโบลา’ คืออะไร อธิบายสั้นๆ ได้ว่าพาราโบลานั้นเป็นทฤษฎีทางคณิตศาสตร์ที่ศึกษาเกี่ยวกับเส้นโค้ง โดยเส้นโค้งนี้เกิดจากการตัดพื้นผิวของกรวยด้วยระนาบที่ขนานกับเส้นกำเนิดกรวย (generating line)
ของพื้นผิวนั้น เส้นโค้งที่เกิดขึ้นนี้จึงเป็นเซตของจุดบนระนาบนั่นเอง 

ทฤษฎีพาราโบลานี้สามารถมาประยุกต์ใช้กับสิ่งต่างๆ ในชีวิตประจำวันได้มากมาย เช่น การโยนวัตถุต่างๆ ขึ้นไปกลางอากาศ วิถีการเดินทางของวัตถุนั้นจะค่อยๆขึ้นและก็ตกลงมา ซึ่งวิถีนั้นก็มีลักษณะเป็นเส้นโค้งแบบพาราโบลาด้วย 

ภาคตัดกรวย (Conic Sections)

เคยเห็นแก้วกระดาษสำหรับดื่มน้ำทรงกรวยกันมั้ย ลองนึกภาพตามว่าถ้าเราเอากระดาษไปผ่าแก้วทรงกรวยนี้ รูปบนหน้าตัดนั้น เราจะมองเห็นเป็นรูปอะไรได้บ้าง 

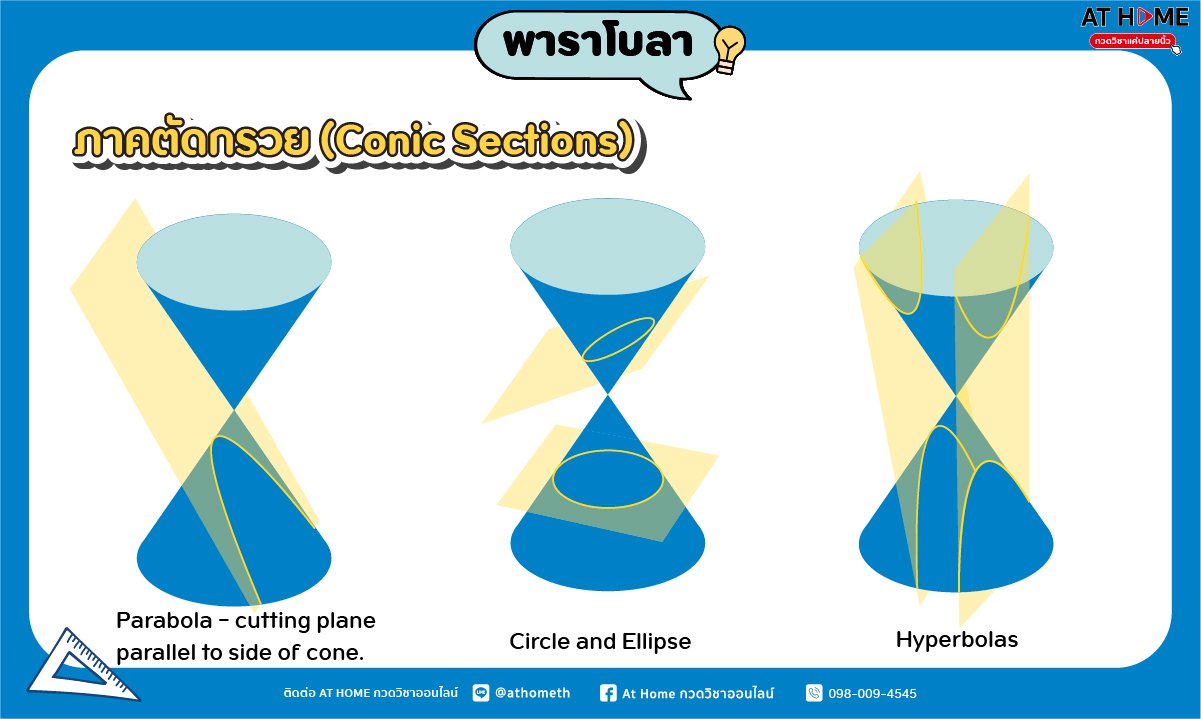
จากภาพบน การตัดกรวย ที่แนวระนาบที่ต่างกันก็จะได้รูปของภาคตัดกรวยที่ต่างกัน ถ้าระนาบตัดกรวยในแนวขนานกับเส้นขอบของกรวย หรือ เส้นกำเนิดกรวย จะเกิดเส้นโค้งที่เราเรียกว่า “พาราโบลา” แต่ถ้าระนาบตัดกรวยตัดในแนวอื่นๆ ก็จะเกิด วงกลม วงรี หรือไฮเปอร์โบลา นั่นเอง 

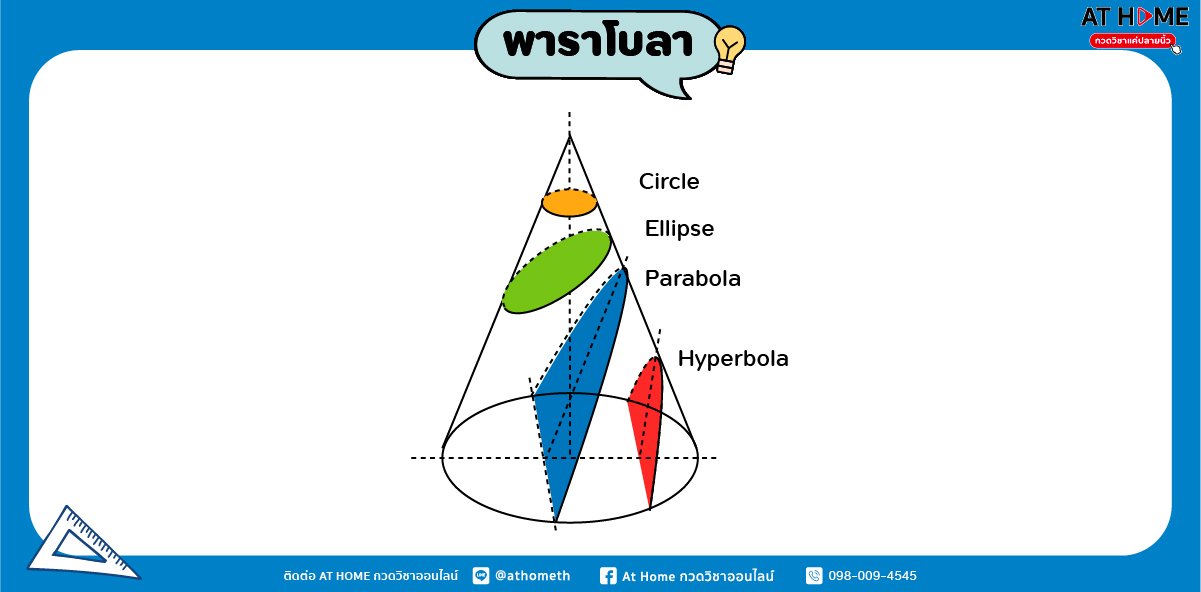
ส่วนประกอบของพาราโบลา

หากเราวาดเส้นโค้งพาราโบลาบนระนาบของแกน x และแกน y เป็นกราฟเส้นโค้งดังรูป เราจะเห็นส่วนประกอบของพาราโบลาดังต่อไปนี้ 

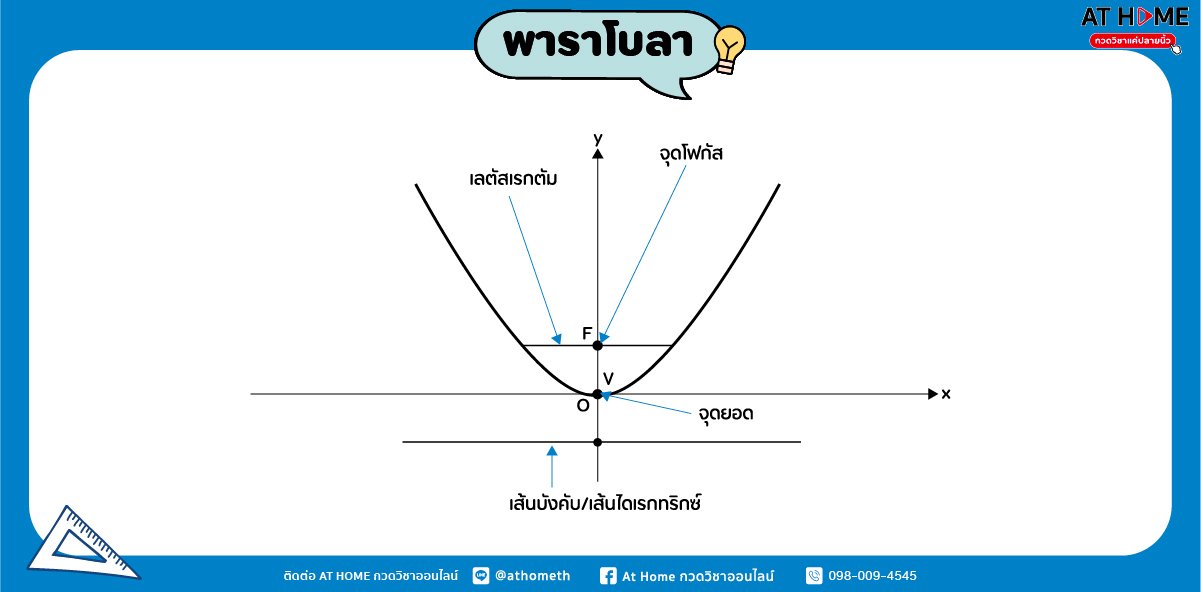
จุดยอด หรือ จุดยอดพาราโบลา

จุดยอดเป็นส่วนประกอบของพาราโบลา ใช้สัญลักษณ์ “V” แทนคำว่า Vertex
เป็นจุดยอดที่พาราโบลาตัดกับแกนของพาราโบลา หรือจุดที่อยู่กึ่งกลางระหว่างจุดโฟกัสกับเส้นไดเรกตริกซ์

เส้นไดเรกตริกซ์ (Directrix)

เส้นไดเรกตริกซ์ของพาราโบลา หรือเรียกกันว่า “เส้นคงที่” เป็นเส้นตรงที่อยู่คู่กับจุดโฟกัส
ใช้สำหรับกำหนดหรือบังคับเซตของจุดชุดหนึ่งให้เรียงต่อกันเป็นเส้นโค้งพาราโบลาในระบบภาคตัดกรวย 

เลตัสเรกตัม

เลตัสเรกตัม คือ ส่วนของเส้นตรงที่ลากผ่านจุดโฟกัส และมีจุดปลายทั้งสองอยู่บนพาราโบลา
ปลายด้านหนึ่งคือ A และปลายอีกด้านคือ B จึงใช้สัญลักษณ์ว่า AB เป็นเส้นที่แสดงความกว้างของพาราโบลา ณ จุดโฟกัส และเลตัสเรกตัมจะตั้งฉากกับแกนของพาราโบลาเสมอ 

จุดโฟกัส

จุดโฟกัสหรือจุดคงที่ ใช้สัญลักษณ์ F เมื่อพาราโบลาคือเซตของจุดทั้งหมดในระนาบซึ่งมีระยะห่างจากจุดที่กำหนดและเส้นที่กำหนดเท่ากัน จุดที่กำหนดนี้เรียกว่า จุดโฟกัส และเส้นที่กำหนดนี้เรียกว่าเส้นไดเรกตริกซ์

จุดกำเนิด

จากรูปกราฟพาราโบลา จุดกำเนิด คือ จุดที่แกน x และแกน y มีค่าเท่ากับ 0 หรือ
จุดที่ทั้งสองแกนตัดกันนั่นเอง 

แกนของพาราโบลา

พาราโบลาคือ เส้นตรงที่ลากผ่านจุดโฟกัสและไปตั้งฉากกับเส้นไดเรกตริกซ์ (Directrix) เราจะเรียกว่าแกนของพาราโบลา

สมการพาราโบลา

สมการของพาราโบลาเป็นสมการที่สามารถเขียนให้อยู่ในรูป           
( รอเเก้เลขยกกำลัง )  

                            y=ax2+bx+c

เมื่อ a, b, c เป็นค่าคงตัว (คือตัวเลขในรูปแบบต่างๆ)

และ a0 เพราะถ้า a เป็น 0 ก็จะทำให้กำลังสองหายไป 

จุดสังเกตง่ายๆว่าสมการใดเป็นสมการของพาราโบลา สมการนั้นจะต้องเป็นสมการกำลังสอง ซึ่งจะมี x2 ปรากฎอยู่ในสมการเสมอ

ตัวอย่างสมการพาราโบลา

y=3×2+6x+1

สมการพาราโบลานี้มีค่า a=3, b=6, c=1

y=-2×2-12x-17

สมการพาราโบลานี้มีค่า a=-2, b=-12, c=-17

y=4×2-5

สมการพาราโบลานี้มีค่า a=4, b=0, c=-5

y= 4x-x22 เราสามารถเขียนสมการนี้ใหม่ได้ว่า y=4×2-x22 

สมการพาราโบลานี้มีค่า a=12, b=2, c=0

y=6-x2

สมการพาราโบลานี้มีค่า a=-1, b=0, c=6

y=3x-5

สมการนี้ไม่ใช่สมการของพาราโบลา เพราะไม่สามารถจัดให้อยู่ในรูป y=ax2+bx+c ได้

y=x2(x-1) เราสามารถเขียนสมการนี้ใหม่ได้ว่า y=x3-x2

สมการนี้ไม่ใช่สมการของพาราโบลา เพราะไม่สามารถจัดให้อยู่ในรูป y=ax2+bx+c ได้

กราฟพาราโบลา

กราฟของพาราโบลาหรือกราฟของฟังก์ชันกำลังสอง การเขียนกราฟของสมการพาราโบลา
นิยมเขียนสมการให้อยู่ในรูป ( รอเเก้เลขยกกำลัง )  

              y=a(x-h)2+k   เมื่อ  a0

ซึ่งเป็นการทำบางส่วนของสมการ y=ax2+bx+c ให้เป็นกำลังสองสมบูรณ์ดังนี้ 

จากสมการดังกล่าวเราสามารถสรุปเป็นสูตรของพาราโบลาได้ดังนี้

สูตรของพาราโบลา