แคลคูลัสเบื้องต้น คือ สาขาหลักของคณิตศาสตร์ซึ่งพัฒนามาจากพีชคณิต เราขาคณิต และปัญหาทางฟิสิกส์ โดยมีต้นกำเนิดจากสองแนวคิดหลัก ดังนี้ แคลคูลัสเชิงอนุพันธ์ (Differential Calculus) เป็นทฤษฎีที่ว่าด้วยอัตราการเปลี่ยนแปลง และเกี่ยวข้องกับการหาอนุพันธ์ของฟังก์ชั่นทางคณิตศาสตร์ แนวคิดที่สองคือ แคลคูลัสเชิงปริพันธ์ (Integral Calculus) เป็นทฤษฎีที่ได้แรงบันดาลใจจากการคำนวณหาพื้นที่หรือปริมาตรของรูปทรงทางเรขาคณิตต่าง ๆ
ลิมิตของฟังก์ชัน
บทนิยาม

ทฤษฎีบทเกี่ยวกับลิมิต
เมื่อ a เป็นจำนวนจริงใด ๆ
1.ถ้า f(x) = c เมื่อ c เป็นค่าคงตัวใด ๆ แล้ว
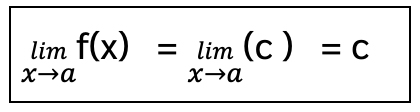
2.ถ้า f(x) = xn เมื่อ n เป็นจำนวนเต็มบวกแล้ว
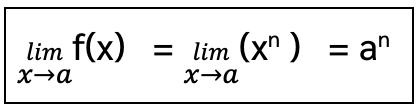
3.เมื่อ L และ M เป็นจำนวนจริงใด f และ g เป็นฟังก์ชันที่มีโดเมนและเรนจ์เป็นสับเซตของจำนวนจริง

4. ถ้า f(x) = cn xn + cn-1 x n-1 + …..+ c1 x + c0 เป็นฟังก์ชันพหุนามแล้ว
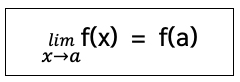
5. ถ้า f เป็นฟังก์ชันตรรกยะโดยที่ f(x) = g(x)h(x) เมื่อ g(x) และ h(x) เป็นฟังก์ชันพหุนามแล้ว

6. เมื่อ L เป็นจำนวนจริงใด ๆ f และ g เป็นฟังก์ชันที่มีโดเมนและเรนจ์เป็นสับเซตของจำนวนจริง

7. เมื่อ f และ g เป็นฟังก์ชันที่โดเมนและเรนจ์เป็นสับเซตของจำนวนจริง
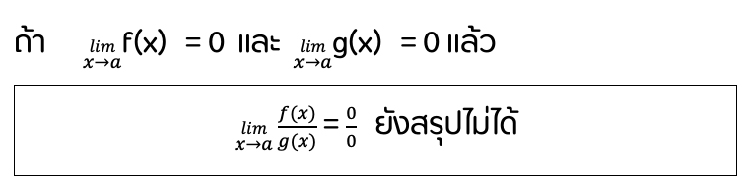
ดังนั้น การหาลิมิตของฟังก์ชันประเภทนี้ต้องพยายามกำจัดรูป 00 ทิ้ง จนกระทั่งไม่อยู่ในรูป 00
โดยอาจใช้วิธี
- แยกตัวประกอบ
- คูณด้วยเทอมที่เป็นสังยุค
นอกจากนี้อาจใช้วิธีอื่นได้อีก เช่น กฎของโลปิตาล
อนุพันธ์ของฟังก์ชัน

บทนิยาม
- เรากล่าวว่า f มีอนุพันธ์บนช่วงเปิด (a,b) ก็ต่อเมื่อ f มีอนุพันธ์ ทุก ๆ จุด x (a,b)
- เรากล่าวว่า f มีอนุพันธ์บนช่วงเปิด [a,b] ก็ต่อเมื่อ f มีอนุพันธ์บนช่วงเปิด (a,b) f
มีอนุพันธ์ทางขวาที่ x = a และ f มีอนุพันธ์ทางซ้ายที่ x = b
อนุพันธ์ของ f ที่ x = a เขียนแทนด้วย f’(a)

บทนิยาม
f’(a) = xaf(a+h) – f(a)h เมื่อลิมิตมีค่า
ถ้าให้ x = a + h เมื่อ h → 0 จะได้ว่า x → a ดังนั้นเราสามารถสรุปเป็นทฤษฎีบทได้ดังนี้
ทฤษฎีบท
f’(a) = xaf(x) – f(a)x-a เมื่อลิมิตมีค่า
และ xaf(x) – f(a)x-a จะหาค่าได้ก็ต่อเมื่อ
xa-f(x) – f(a)x-a = xa+f(x) – f(a)x-a
ทฤษฎีบท
ถ้า f มีอนุพันธ์ที่ x =a แล้ว f จะมีความต่อเนื่องที่ x = a
สรุป
- ถ้า f มีอนุพันธ์ที่ x = a แล้ว f ก็ต่อเนื่องที่ x = a
- ถ้า f ไม่ต่อเนื่องที่ x = a แล้ว f จะไม่มีอนุพันธ์ที่ x = a
- ถ้า f ต่อเนื่องที่ x = a แล้วอาจจะมีหรือไม่มีอนุพันธ์ที่ x = a
อัตราการเปลี่ยนแปลง

การหาอนุพันธ์ของฟังก์ชันพีชคณิตโดยใช้สูตร

กฎของโลปิตาล
ให้ f และ g เป็นฟังก์ชันที่หาอนุพันธ์ได้โดยที่ g’(x) 0 และ a R
ถ้า xaf(x) = 0 และ xag(x) = 0 แล้ว
| xaf(x) g(x) = xaf'(x) g'(x) |
เมื่อ xaf'(x)g'(x) หาค่าได้
ถ้า xaf'(x)g'(x) อยู่รูป 00 ให้ทำซ้ำได้อีกจนสามารถหาค่าลิมิตได้
อนุพันธ์ของฟังก์ชันประกอบ

ความชันของเส้นโค้ง
ถ้า y = f(x) เป็นสมการเส้นโค้ง และ f หาอนุพันธ์ได้ที่ x
- ความชันของเส้นสัมผัสเส้นโค้งที่จุด (x,y) ใด ๆ = f’(x)
- ความชันของเส้นสัมผัสเส้นโค้งที่จุด (x1, y1) = f’(x1)
- ความชันของเส้นปกติที่จุด (x1,y1) = -1f’(x1) , f’(x1) 0
- สมการของเส้นตรงที่มีความชัน = m และผ่านจุด (x1,y1) คือ y-y1 = m(x-x1)
อนุพันธ์อันดับสูง

การประยุกต์ของอนุพันธ์
- ฟังก์ชันเพิ่มและฟังก์ชันลด
บทนิยาม
ฟังก์ชัน f เป็นฟังก์ชันเพิ่มบนช่วง I ถ้าสำหรับสองจำนวน x1,x2 ใด ๆ ในช่วง I
ซึ่ง x1 < x2 แล้ว f(x1) < f(x2)
ฟังก์ชัน f เป็นฟังก์ชันลดบนช่วง I ถ้าสำหรับสองจำนวน x1, x2 ใด ๆ
ในช่วง I ซึ่ง x1 < x2 แล้ว f(x1) > f(x2)
| กฎข้อที่ 1 f สามารถหาอนุพันธ์ได้ในช่วง (a,b)ถ้า f’(x) > 0 สำหรับทุก ๆ x ใน (a,b)แล้ว f จะเป็นฟังก์ชันเพิ่มบนช่วง (a,b) ถ้า f’(x) < 0 สำหรับทุก ๆ x ในช่วง (a,b)แล้ว f จะเป็นฟังก์ชันลดบนช่วง (a,b) |
- ค่าสูงสุดสัมพัทธ์และค่าต่ำสุดสัมพัทธ์ของฟังก์ชัน
บทนิยาม
ฟังก์ชัน f จะมีค่าสูงสุดสัมพัทธ์ที่ x = x0 ถ้ามีช่วงเปิด (a,b) ซึ่ง x0 (a,b)
และ f(x0) f(x) สำหรับทุก ๆ x (a,b) และค่าสูงสุดสัมพัทธ์คือ f(x0)
ฟังก์ชัน f จะมีค่าต่ำสุดสัมพัทธ์ที่ x = x0 ถ้ามีช่วงเปิด (a,b) ซึ่ง x0 (a,b)
และ f(x0) f(x) สำหรับทุก ๆ x (a,b) และค่าต่ำสุดสัมพัทธ์คือ f(x0)
| กฎข้อที่ 2 ถ้าฟังก์ชัน f มีค่าสูงสุดสัมพัทธ์หรือต่ำสุดสัมพัทธ์เมื่อ x = x0 และ x0 Df แล้ว f’(x0) = 0 หรือ f’(x0) หาค่าไม่ได้ |
บทนิยาม
ถ้า x0 อยู่ในโดเมนของ f โดยที่ f’( x0) = 0 หรือ f’( x0) หาค่าไม่ได้ แล้วจะเรียก x0 ว่าค่าวิกฤตของ f ถ้า x0 เป็นค่าวิกฤตของ f แล้วเรียกจุด (x0 , f(x0 )) ว่าจุดวิกฤต
- ค่าสูงสุดสัมบูรณ์และค่าต่ำสุดสัมบูรณ์ของฟังก์ชัน
บทนิยาม
- ฟังก์ชัน f มีค่าสูงสุดสัมบูรณ์ ที่ x = x0
ถ้า f( x0 ) f(x) สำหรับทุก x ในโดเมนของ f แล้วเราจะเรียก f(x0) ว่าเป็นค่าสูงสุดสัมบูรณ์ของ f
- ฟังก์ชัน f มีค่าต่ำสุดสัมบูรณ์ ที่ x = x0
ถ้า f(x0) f(x) สำหรับทุก x ในโดเมนของ f แล้วเราจะเรียก f(x0) ว่าเป็นค่าต่ำสุดสัมบูรณ์ของ f
ปฏิยานุพันธ์
ให้ f เป็นฟังก์ชันที่กำหนดให้ และ F เป็นฟังก์ชันที่มีอนุพันธ์เท่ากับ f นั่นคือ F’(x) = f(x)
บทนิยาม
ฟังก์ชัน F ซึ่ง F’(x) = f(x) สำหรับทุก x ว่าเป็น “ปฏิยานุพันธ์ของฟังก์ชัน f”
ปริพันธ์ไม่จำกัดเขต
สัญลักษณ์แทนการหาปฏิยานุพันธ์ของ f(x) ได้เป็น f(x)d(x) อ่านว่า
“ปริพันธ์ไม่จำกัดเขตของฟังก์ชัน f เทียบกับตัวแปรx”
| ถ้า F’(x) = f(x) แล้วจะได้ f(x) dx = F(x) + c เมื่อ c เป็นค่าคงตัว |
สรุป แคลคูลัส สั้น ๆ หาปริพันธ์ไม่จำกัดเขต
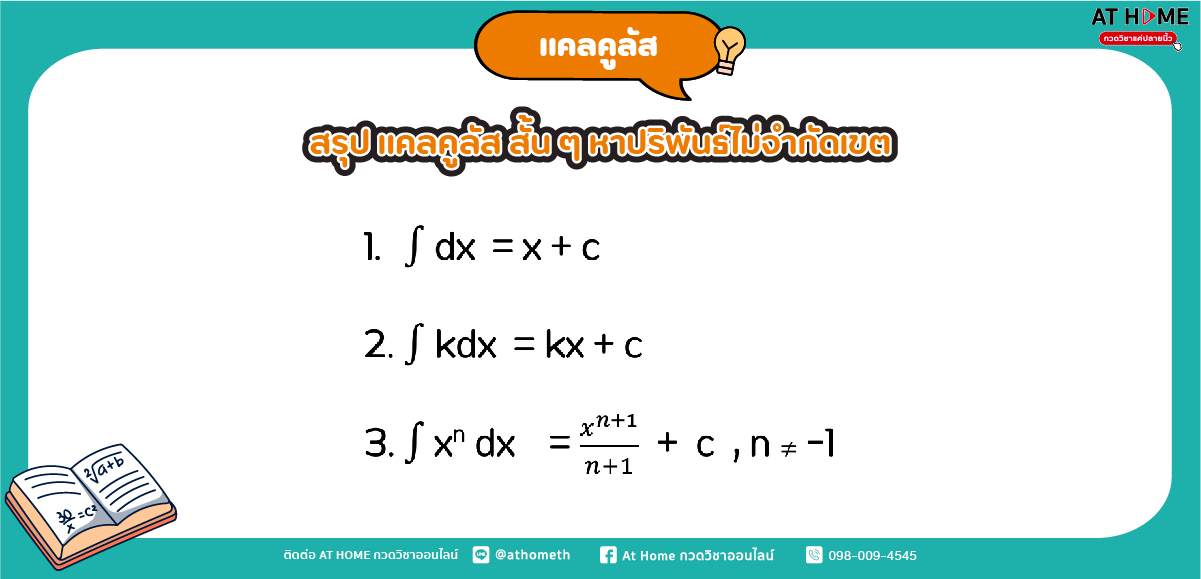
อินทิเกรดจำกัดเขต

การหาพื้นที่ใต้เส้นโค้ง แคลคูลัส สรุป
ขั้นตอนการหาพื้นที่ใต้กราฟ
- หาจุดตัดแกน x
- คำนวณหาพื้นที่ในแต่ละส่วน
คำถามที่พบบ่อย (FAQ)
แคลคูลัส 1 ประกอบด้วยเรื่อง
แคลคูลัสคือ เนื้อหาแคลคูลัสระดับมหาลัย ประกอบด้วยเรื่อง ลิมิตและความต่อเนื่อง / อนุพันธ์ / การอินทิเกรต / ฟังก์ชันอดิศัย / การประยุกต์อนุพันธ์ / เทคนิคการอินทิเกรต / การประยุกต์ของอินทิกรัล / อินทิกรัลไม่ตรงแบบ
แคลคูลัส 2 ประกอบด้วย
ลำดับและอนุกรมของจำนวน / อนุกรมกำลัง / ปริภูมิสามมิติ / ระบบพิกัดเชิงขั้ว
/ ฟังก์ชันค่าจริงของหลายตัวแปร / อินทิกรัลของฟังก์ชันของสองตัวแปร / สมการเชิงอนุพันธ์เบื้องต้น
แคลคูลัส ม.6 ต่างกับ แคลคูลัส มหาลัย ยังไง
แคลคูลัส ม.6 เป็นเนื้อหาเบื้องต้นที่เป็นส่วนหนึ่งของแคลคูลัส แต่แคลคูลัสระดับมหาวิทยาลัยจะกว้างและลึกกว่า บางมหาวิทยาลัยจะสอนต่างกัน รวมไปถึงแต่ละคณะก็ต่างกัน
แคลคูลัสยากมั้ย
ไม่ยากหากเข้าใจบทนิยามต่าง ๆ และประยุกต์ใช้เป็น





