รูปร่าง และ รูปทรง เป็นสิ่งที่เราพบเห็นกันบ่อยมาก ๆ ในแต่ละวัน แต่น้อง ๆ หลายคนอาจจะสับสนกับสองคำนี้อยู่ว่าต่างกันยังไง พี่ ๆ ATHOME จึงอยากจะช่วยไขข้อสงสัยเหล่านั้น ด้วยโน้ตสรุปรวบยอดความเข้าใจแบบครบถ้วนมาให้ค่ะ
รูปร่างและรูปทรง คืออะไร ต่างกันตรงไหน
รูปร่างและรูปทรง หมายถึง รูปเรขาคณิตที่มีความสัมพันธ์และความแตกต่างกันโดยที่ รูปร่าง (Shape) เป็น เส้นของรอบของวัตถุนั้น ๆ ไม่ว่าจะเป็นสิ่งที่เป็นธรรมชาติหรือที่มนุษย์สร้างขึ้นก็ตาม มีเพียง 2 มิติ เท่านั้น คือ ด้านกว้างและด้านยาว กล่าวง่าย ๆ คือ รูปร่างเป็นสิ่งที่มองเห็นเป็นลักษณะแบน ๆ ส่วนรูปทรง (Form) เป็น โครงสร้างของสิ่งต่าง ๆ มีลักษณะเป็น 3 มิติ คือ มีด้านกว้าง ด้านยาว และด้านสูง หรือความลึก นั่นทำให้มีพื้นที่และปริมาตรภายใน
รูปร่างและรูปทรงมีกี่ประเภท
รูปร่าง แบ่งเป็น 3 ประเภท ได้แก่
- รูปร่างธรรมชาติ (Natural Shape)
เป็นรูปร่างที่เกิดขึ้นเองตามธรรมชาติที่เราพบเห็นได้ เช่น รอยขีดข่วน รอยหิน รอยเท้าสัตว์
- รูปร่างเรขาคณิต (Geometrical Shape)
เป็นรูปร่างที่มีโครงสร้างที่แน่นอน เช่น วงกลม สามเหลี่ยม สี่เหลี่ยม เป็นต้น
- รูปร่างอิสระ (Free Shape)
เป็นรูปร่างที่เกิดขึ้นจากจินตนาการและความต้องการของผู้สร้างสรรค์ ไม่มีรูปแบบที่ตายตัว
รูปทรง แบ่งเป็น 3 ประเภท ได้แก่
- รูปทรงธรรมชาติ (Organic Form)
เป็นรูปทรงแบบสามมิติที่เราพบเห็นได้ในธรรมชาติ เช่น รูปทรงของมนุษย์ รูปทรงของสัตว์ รูปทรงของดอกไม้
- รูปทรงเรขาคณิต (Geometric Form)
เป็นรูปทรงที่มีโครงสร้างที่แน่นอน สามารถแสดงความลึก มีเนื้อที่ มีปริมาตร เช่น ทรงกลม ทรงกรวย ทรงพีระมิด เป็นต้น
- รูปทรงอิสระ (Free Form)
เป็นรูปทรงที่เกิดขึ้นอย่างอิสระ ไม่มีรูปแบบตายตัวแน่นอน เช่น รูปทรงของก้อนเมฆ รูปทรงกระแสน้ำ รูปทรงของกระแสลม เป็นต้น
น้อง ๆ ก็ได้ทราบกันไปแล้วนะคะว่ารูปร่างและรูปทรงมีความแตกต่างกัน และมีหลายประเภท แต่ในวันนี้พี่ ๆ ATHOME อยากจะมาพาน้อง ๆ ไปทำความรู้จักกับรูปร่างและรูปทรงเรขาคณิตให้มากขึ้น รวมถึงสามารถหาพื้นที่และพื้นที่ผิวของรูปร่างและรูปทรงทางเรขาคณิตได้ด้วย ถ้าพร้อมแล้วมาดูไปพร้อมกันเลยค่า!
การหาพื้นที่รูปร่างเรขาคณิต
อย่างที่เราทราบกันว่ารูปร่างเรขาคณิตนั้นมีลักษณะรูปร่างที่แน่นอน ทำให้การหาพื้นที่นั้นก็มีรูปแบบเช่นเดียวกัน โดยเราจะใช้เป็นสูตรในการคำนวณ ซึ่งช่วยให้เราหาพื้นที่ได้อย่างแม่นยำมากขึ้นนั่นคือ ก่อนอื่นเรามาทำความรู้จักกับรูปร่างเรขาคณิตแต่ละรูปแบบก่อนดีกว่าว่ามีอะไรบ้าง
รูปร่างสี่เหลี่ยม (Square)
คือ รูปร่างเรขาคณิตที่มีด้านประกอบ 4 ด้าน มุมภายในรวมได้ 360 องศา
สี่เหลี่ยมมีประเภทไหนบ้าง?




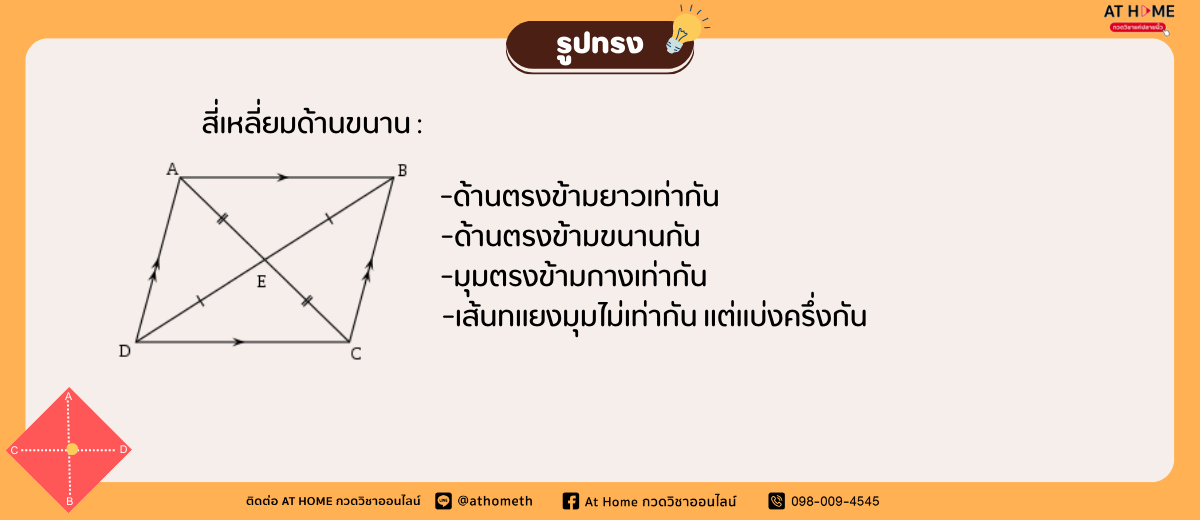
การหาพื้นที่รูปร่างสี่เหลี่ยมจัตุรัส
สูตร ด้าน x ด้าน
ตัวอย่าง รูปสี่เหลี่ยมจัตุรัสมีความยาวแต่ละด้านเท่ากับ 5 เซนติเมตร พื้นที่สี่เหลี่ยมเท่ากับเท่าใด
วิธีทำ จากสูตรพื้นที่สี่เหลี่ยมจัตุรัส = ด้าน x ด้าน
จะได้ พื้นที่สี่เหลี่ยม = 5 x 5 = 25 ตารางเซนติเมตร
การหาพื้นที่รูปร่างสี่เหลี่ยมผืนผ้า
สูตร กว้าง x ยาว
ตัวอย่าง รูปสี่เหลี่ยมผืนผ้า กว้าง 12 เมตร ยาว 20 เมตร จะมีพื้นที่เท่าใด
วิธีทำ จากสูตรพื้นที่สี่เหลี่ยมผืนผ้า = กว้าง x ยาว
จะได้ พื้นที่สี่เหลี่ยมผืนผ้า = 12 x 20 = 240 ตารางเมตร
การหาพื้นที่รูปร่างสี่เหลี่ยมขนมเปียกปูน
สูตร ฐาน x สูง หรือ 1/2 x ผลคูณของเส้นทแยงมุม
ตัวอย่าง รูปสี่เหลี่ยมขนมเปียกปูน มีฐานยาว 11 มิลลิเมตร สูง 13 มิลลิเมตร มีพื้นที่เท่าใด
วิธีทำ จากสูตรพื้นที่สี่เหลี่ยมขนมเปียกปูน = ฐาน x สูง
จะได้ พื้นที่สี่เหลี่ยมขนมเปียกปูน = 11 x 13 = 143 ตารางมิลลิเมตร
การหาพื้นที่รูปร่างสี่เหลี่ยมรูปว่าว
สูตร 1/2 x ผลคูณของเส้นทแยงมุม
ตัวอย่าง รูปสี่เหลี่ยมรูปว่าว มีเส้นทแยงมุมด้านยาวยาว 10 เมตร เส้นทแยงมุมอีกเส้นยาว 20 เมตร
พื้นที่ของสี่เหลี่ยมรูปว่าวจะเท่ากับเท่าใด
วิธีทำ จากสูตรพื้นที่สี่เหลี่ยมรูปว่าว = 1/2 x ผลคูณของเส้นทแยงมุม
จะได้ พื้นที่สี่เหลี่ยมรูปว่าว = ½ x 10 x 20 = 100 ตารางเมตร
การหาพื้นที่รูปร่างสี่เหลี่ยมด้านขนาน
สูตร ฐาน x สูง
ตัวอย่าง ผืนผ้าเป็นรูปสี่เหลี่ยมด้านขนาน มีฐานยาว 30 เซนติเมตร ระยะห่างจากฐานยาว 12 เซนติเมตร พื้นที่ของผืนผ้านี้เท่ากับเท่าใด
วิธีทำ จากสูตรพื้นที่สี่เหลี่ยมด้านขนาน = ฐาน x สูง
จะได้ พื้นที่สี่เหลี่ยมด้านขนาน = 30 x 12 = 360 ตารางเซนติเมตร
รูปร่างสามเหลี่ยม (Triangle)
คือ รูปร่างเรขาคณิตที่มีด้านประกอบ 3 ด้าน มุมภายในรวมได้ 180 องศา
สามเหลี่ยมมีประเภทไหนบ้าง?
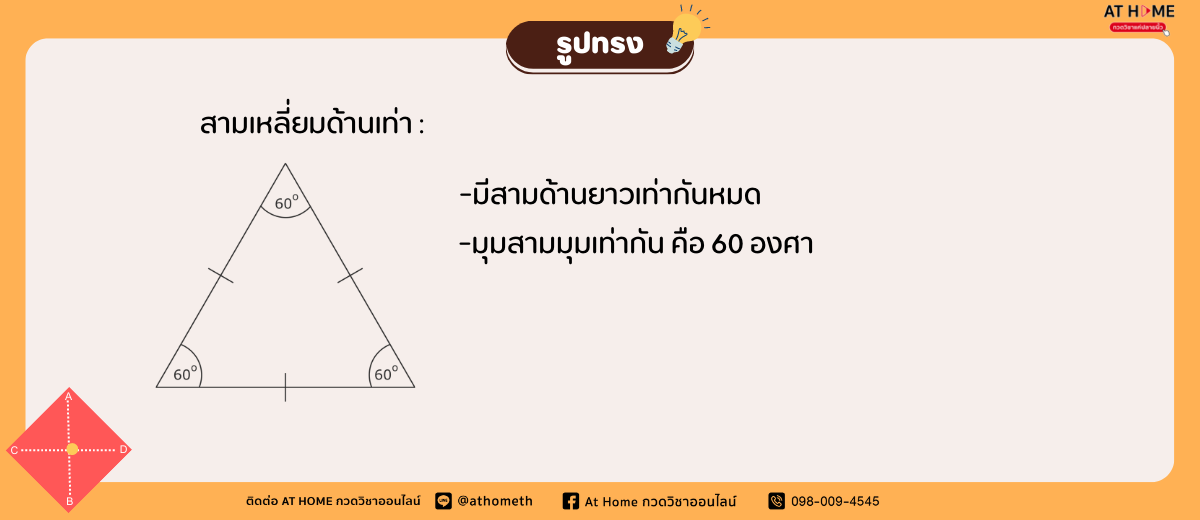

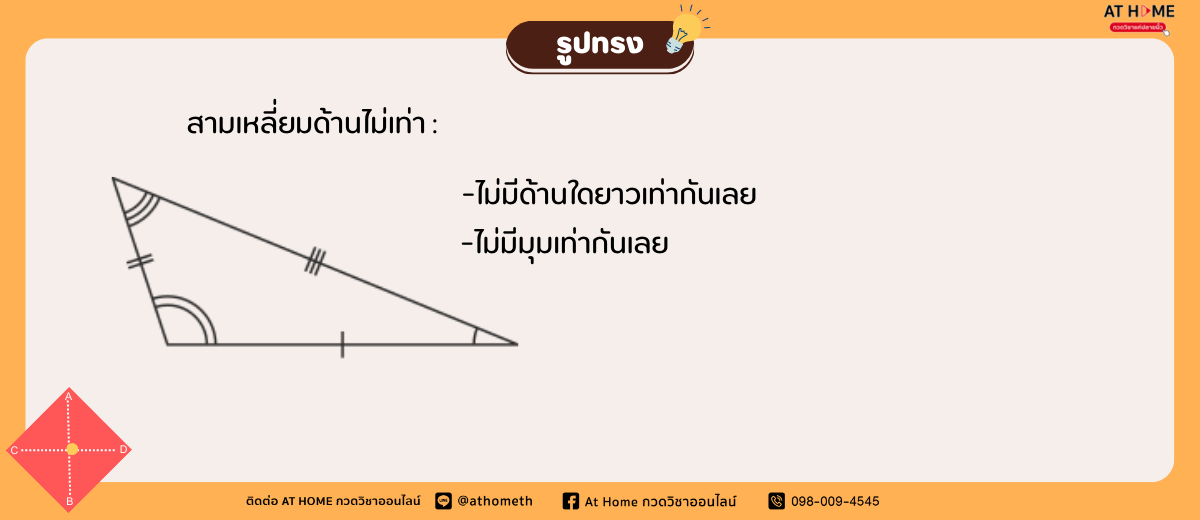
การหาพื้นที่รูปร่างสามเหลี่ยมด้านเท่า
สูตร 34 x ด้าน2
ตัวอย่าง หน้าพิซซ่าเป็นทรงสามเหลี่ยมด้านเท่า ที่แต่ละด้านยาว 10 เซนติเมตร พื้นที่ของพิซซ่าชิ้นนี้เท่ากับเท่าใด
วิธีทำ จากสูตร 34 x ด้าน2
จะได้ พื้นที่พิซซ่า = 34 x 102
จะได้ = 253 ตารางเซนติเมตร
( รอใส่ root )
การหาพื้นที่รูปร่างสามเหลี่ยมหน้าจั่ว
สูตร ½ x ฐาน x สูง
ตัวอย่าง สามเหลี่ยมรูปหนึ่ง มีฐานเท่ากับ 10 หน่วย สูง 12 หน่วย พื้นที่เท่ากับเท่าใด
วิธีทำ จากสูตรพื้นที่สามเหลี่ยม = ½ x ฐาน x สูง
จะได้ พื้นที่สามเหลี่ยมหน้าจั่ว = ½ x 10 x 12 = 60 ตารางหน่วย
การหาพื้นที่รูปร่างสามเหลี่ยมด้านไม่เท่า
สูตร s(s-a)(s-b)(s-c)
เมื่อ S = a + b + c2 โดยที่ a , b , c คือ ด้านของสามเหลี่ยม
ตัวอย่าง สามเหลี่ยมรูปหนึ่ง มีด้านไม่เท่ากันเลยทั้งสามด้าน แต่ละด้านยาว 3 , 3.5 , 4 หน่วย มีพื้นที่เท่าไร
วิธีทำ จากสูตรพื้นที่สามเหลี่ยม = s(s-a)(s-b)(s-c)
จะได้ = 5.25(5.25-3)(5.25-3.5)(5.25-4)
= 5.25(2.25)(1.75)(1.25) = 11.28 ตารางหน่วย
( รอใส่ root )
รูปร่างวงกลม (Circle)
คือ รูปร่างทางเรขาคณิตรูปแบบหนึ่ง เป็นรูปปิด ไม่มีมุม
วงกลมมีประเภทไหนบ้าง?



การหาพื้นที่รูปร่างวงกลมเต็มวง
สูตร r2 = d2 / 4
ตัวอย่าง จากรูปที่กำหนดให้ พื้นที่วงกลมเท่ากับเท่าใด
วิธีทำ จากสูตรพื้นที่วงกลม = r2
จะได้ พื้นที่วงกลม = (2)(2) = 4 ตารางเซนติเมตร
( รอใส่ พายอาร์)
การหาพื้นที่รูปร่างวงกลมครึ่งวง
สูตร r22
ตัวอย่าง จากรูปที่กำหนดให้ พื้นที่ครึ่งวงกลมเท่ากับเท่าใด
วิธีทำ จากสูตรพื้นที่วงกลม = r2 แต่โจทย์เป็นครึ่งวงกลมเราจึงหาร 2
จากโจทย์ d = 8 ซม. / r = 4 ซม.
จะได้ พื้นที่ครึ่งวงกลม = r22 = 8
( รอใส่ พายอาร์)
การหาพื้นที่รูปร่างวงกลม1/4 วง
สูตร r24
ตัวอย่าง จากรูปที่กำหนดให้ พื้นที่ครึ่งวงกลมเท่ากับเท่าใด
วิธีทำ จากสูตรพื้นที่วงกลม = r2 แต่โจทย์เป็น ¼ วงกลมเราจึงหาร 4
จากโจทย์ r = 10 ซม.
จะได้ พื้นที่ครึ่งวงกลม = r24 = 25
( รอใส่ พายอาร์)
รูปร่างห้าเหลี่ยม (Pentagon)
คือ รูปหลายเหลี่ยมที่มี 5 ด้าน มุมภายในรวม 540 องศา
รูปห้าเหลี่ยมมีประเภทไหนบ้าง?
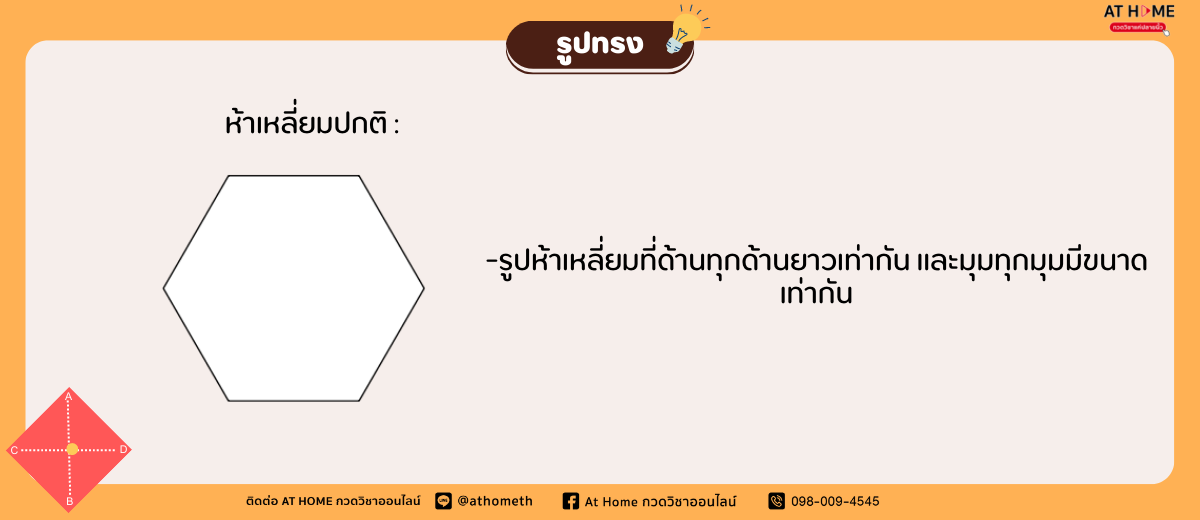
การหาพื้นที่รูปร่างห้าเหลี่ยมปกติ
สูตร 1.72 x (ด้าน)2
ตัวอย่าง จากรูปที่กำหนดให้ พื้นที่ห้าเหลี่ยมเท่ากับเท่าใด
วิธีทำ จากสูตรห้าเหลี่ยม = 1.72 x (ด้าน)2
จะได้ พื้นที่ห้าเหลี่ยม = 1.72 x (10)(10) = 172 ตารางเซนติเมตร
รูปร่างหกเหลี่ยม (Hexagon)
คือ รูปหลายเหลี่ยมที่มี 6 ด้าน มุมแต่ละมุมเท่ากับ 120 องศา
รูปหกเหลี่ยมมีประเภทไหนบ้าง?
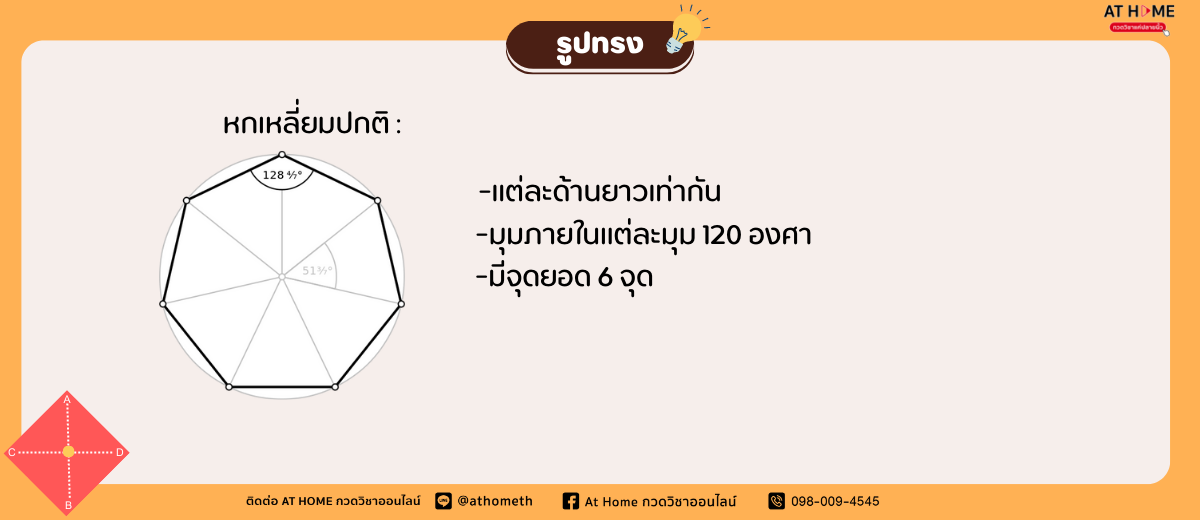
การหาพื้นที่รูปร่างหกเหลี่ยม
สูตร 332 x ด้าน2
ตัวอย่าง จากรูปที่กำหนดให้ พื้นที่หกเหลี่ยมเท่ากับเท่าใด
วิธีทำ จากสูตรหกเหลี่ยม = 332 x ด้าน2
จะได้ พื้นที่หกเหลี่ยม = 332 x (10)(10) = 1503 ตารางเซนติเมตร
( รอใส่ root )
รูปร่างแปดเหลี่ยม (Octagon)
คือ รูปหลายเหลี่ยม มี 8 ด้าน มุมแต่ละมุมกาง 135 องศา
รูปแปดเหลี่ยมมีประเภทไหนบ้าง?
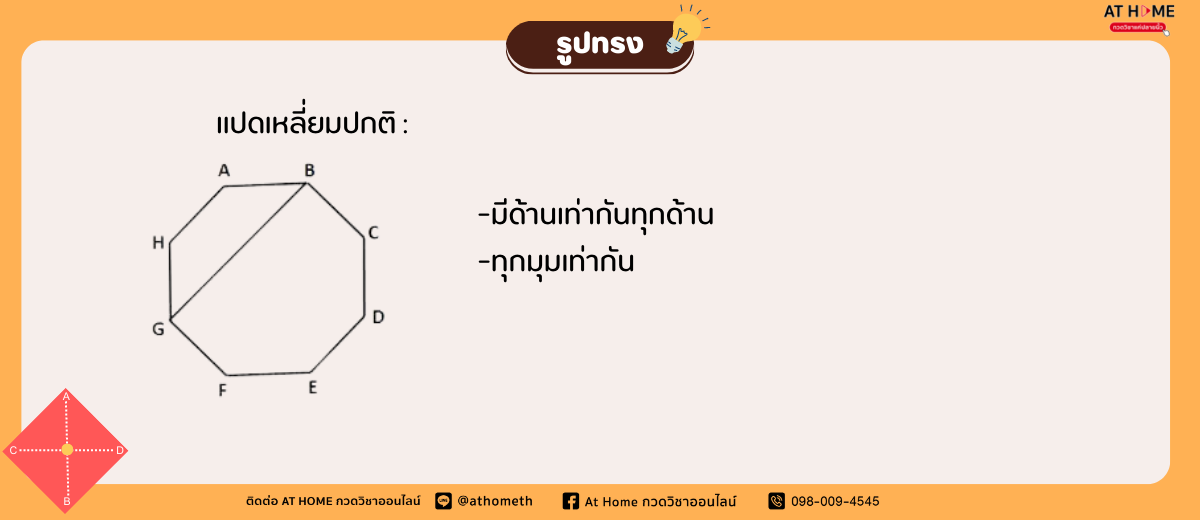
การหาพื้นที่รูปร่างแปดเหลี่ยม
สูตร 4.828 × (ด้าน)2
ตัวอย่าง จากรูปที่กำหนดให้ พื้นที่หกเหลี่ยมเท่ากับเท่าใด
วิธีทำ จากสูตรพื้นที่แปดเหลี่ยม = 4.828 × (ด้าน)2
จะได้พื้นที่แปดเหลี่ยม = 4.828 × 9 = 43.45 ตารางเซนติเมตร
แบบฝึดหัดรูปร่างและรูปทรงพร้อมเฉลย
- แผ่นอิฐรูปสี่เหลี่ยมมุมฉาก มีพื้นที่ 350 ตารางเซนติเมตร แผ่นอิฐยาว 25 เซนติเมตร แผ่นอิฐกว้างกี่
เซนติเมตร
วิธีทำ จากสูตรพื้นที่สี่เหลี่ยมมุมฉาก = กว้าง x ยาว
จากโจทย์ เรารู้พื้นที่ และ ความยาว แต่เขาถามหาความกว้าง
แทนค่าลงในสูตร จะได้ 350 = 25 x ความกว้าง
ความกว้าง = 350 / 25 = 14 เซนติเมตร
- ผ้าผืนหนึ่งเป็นรูปสี่เหลี่ยมจัตุรัส วัดเส้นรอบรูปได้ยาว 300 เซนติเมตร ผ้าผืนนี้มีพื้นที่กี่ตาราง เซนติเมตร
วิธีทำ จากโจทย์ เส้นรอบรูปยาว 300 เซนติเมตร หมายความว่า 4(ด้าน) = 300
ดังนั้น ด้านยาวเท่ากับ 300/4 = 75 เซนติเมตร
จากสูตรพื้นที่สี่เหลี่ยมจัตุรัส = ด้าน x ด้าน
จะได้ = 75 x 75 = 5625 ตารางเซนติเมตร
- กระจกรูปสี่เหลี่ยมผืนผ้ากว้าง 44 เซนติเมตร ยาว 1.5 เมตร ตัดตามแนวทแยงมุมได้ 2 แผ่นเท่าๆ กัน แต่ละแผ่นมีพื้นที่เท่าไร
วิธีทำ จากโจทย์ กว้าง = 44 เซนติเมตร ยาว = 150 เซนติเมตร
จากสูตรพื้นที่ของกระจก = กว้าง x ยาว
จะได้ = 44 x 150 = 6600 ตารางเซนติเมตร
เมื่อตัดกระจกเป็นสองแผ่น พื้นที่แต่ละแผ่นจะเท่ากับ
= 6600 / 2 = 3300 ตารางเซนติเมตร
ดังนั้น พื้นที่กระจกแต่ละแผ่นที่ถูกตัดตามแนวทแยงมุม เท่ากับ 3300 ตารางเซนติเมตร
คำถามที่พบบ่อย (FAQ)
รูปร่างและรูปทรงแตกต่างกันอย่างไร
รูปทรงจะมีมิติมากกว่ารูปร่าง รูปร่างจะไม่มีพื้นที่ภายใน
รูปร่างและรูปทรงมีกี่มิติ
รูปทรงมี 3 มิติ รูปร่างมี 2 มิติ
พื้นที่ผิว ต่างจาก พื้นที่ผิวข้าง หรือไม่
แตกต่างกันโดย พื้นที่ผิวหมายถึงพื้นที่ผิวทั้งหมดของรูปทรงนั้น ๆ โดยรวมพื้นที่ผิวข้างไปด้วย
น้อง ๆ หลายคนที่รู้สึกว่าทำไมบทเรื่องรูปร่างเรขาคณิตสูตรเยอะจัง อย่าเพิ่งท้อถอยไปน้า ไม่มีอะไรที่ยากเกินความตั้งใจของเราอยู่แล้ว ไม่ต้องกดดันตัวเอง แต่ขอให้เชื่อมั่นในความพยายามของตนเองเสมอ จากนั้นหมั่นทบทวนแบบฝึกหัดที่พี่ ๆ นำมาให้นี้อย่างสม่ำเสมอ รับรองว่าน้อง ๆ จะทำบทนี้ได้ดีแน่ ๆ เลยล่ะ





