สรุป ความน่าจะเป็น ม.4-6 สูตร แบบฝึกหัด โจทย์ พร้อมเฉลยแบบเข้าใจง่าย ฟิตก่อนสอบจริง

ในชีวิตประจำวัน เรามักจะได้ยินคำว่า “โอกาส” เช่น โอกาสที่ฝนจะตกเท่ากับ 80% หมายถึง เหตุการณ์ที่ฝนจะตกมากกว่าเหตุการณ์ที่ฝนไม่ตก แต่ถ้าเราโยนเหรียญเที่ยงตรง 1 เหรียญ โอกาสที่เหรียญจะออกหัวหรือก้อยเป็นจำนวนเท่า ๆ กัน คือ 50% ซึ่งสิ่งที่อาจจะเกิดหรือไม่เกิดนั้นเรียกได้ว่าเป็นความน่าจะเป็น ซึ่งเราสามารถคำนวณได้ตามสูตรต่าง ๆ ดังต่อไปนี้

[สรุปความน่าจะเป็น ม.4]

หลักการบวกและการคูณ

ในการที่เราจะนับจำนวนสิ่งของ เหตุการณ์ หรือ จำนวนวิธีในการทำงานบางอย่าง อาจจะสามารถนับได้โดยตรง แต่หากสิ่งที่จะนับมีจำนวนมาก อาจจะทำให้การนับโดยตรงนั้นทำได้ยาก จึงมีหลักการนับ เพื่อช่วยให้การนับสิ่งที่มีจำนวนเยอะ ทำได้ง่ายขึ้น 

หลักการบวก 

หลักการคูณ

การเรียงสับเปลี่ยน

หากมีสิ่งของอยู่ n ชิ้นแตกต่างกัน  หากต้องการจะนำสิ่งของ r ชิ้นจากสิ่งของที่มีอยู่
นำมาเรียงลำดับจะได้ว่า

• ขั้นตอนที่ 1 เลือกของชิ้นที่ 1 มาวาง ซึ่งจะเป็นชิ้นใดก็ได้ มี n ชิ้น
• ขั้นตอนที่ 2 เลือกของชิ้นที่ 2 มาวาง โดยเป็นชิ้นที่เหลือจากการวางชิ้นที่ 1 มี n-1 ชิ้น
• ขั้นตอนที่ r เลือกของชิ้นที่ r โดยเป็นชิ้นที่เหลือจากการวางชิ้นที่ r-1 มี n-r+1 ชิ้น
  

การจัดหมู่

การเลือกกลุ่มของสิ่งของมา โดยไม่คำนึงถึงลำดับในการเรียงของสิ่งของในกลุ่มที่เลือกมา
หากกลุ่มใดมีสิ่งของในกลุ่มเหมือนกัน จะนับเป็นการจัดหมู่เพียง 1 วิธี 

[สรุปความน่าจะเป็น ม.5]

การทดลองสุ่มและเหตุการณ์

การทดลองสุ่ม คือ การทดลองซึ่งทราบว่าผลลัพธ์จะเป็นอะไรบ้าง แต่ไม่สามารถบอกได้ว่า
ในแต่ละครั้งที่ทดลอง ผลที่เกิดขึ้นจะเป็นอะไรในบรรดาผลลัพธ์ที่อาจเป็นไปได้เหล่านั้น

เช่น การทอดลูกเต๋าหนึ่งลูกหนึ่งครั้ง แต้มที่ปรากฏอาจเป็น 1-6 แต่ไม่สามรถบอกได้ว่าจะเป็นเลขใด
เรียกการทอดลูกเต๋าว่า การทดลองสุ่ม และเซตแต้มที่อยู่บนหน้าลูกเต๋าว่า

ความน่าจะเป็น

ความน่าจะเป็น คือ จำนวนที่บอกให้ทราบว่าเหตุการณ์ที่สนใจมีโอกาสเกิดขึ้นมากน้อยเพียงใด

บทนิยาม

ให้ S แทนปริภูมิตัวอย่างซึ่งเป็นเซตจำกัด โดยสมาชิกทุกตัวของ S มีโอกาสเกิดขึ้นเท่ากัน และให้ E เป็นเหตุการณ์ที่เป็นสับเซตของ S 

ความน่าจะเป็นเขียนแทนด้วย P(E)

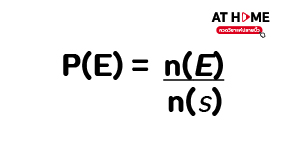
เมื่อ  n(E) แทนจำนวนสมาชิกของเหตุการณ์ E

และ n(s) แทนจำนวนสมาชิกของปริภูมิตัวอย่าง S

สรุปความน่าจะเป็น สมบัติพื้นฐาน

1. สำหรับเหตุการณ์ E ใด ๆ จะได้ว่า 0 น้อยกว่าหรือเท่ากับ  P(E) น้อยกว่าหรือเท่ากับ 1
2. ความน่าจะเป็นของปริภูมิตัวอย่าง S เท่ากับ 1 นั่นคือ P(S) = 1
3. ความน่าจะเป็นของเหตุการณ์ที่เป็นเซตว่างเท่ากับ 0 นั่นคือ P() = 0

ตัวอย่าง

1. ในการเลือกจำนวนสองจำนวนโดยไม่เจาะจงจาก {1,2,3,4,5} โดยเลือกทีละจำนวนไม่ให้ซ้ำกัน จงหาความน่าจะเป็นที่จะได้จำนวนแรกมากกว่า 3

วิธีทำ  

ให้ S แทนปริภูมิตัวอย่างของการทดลองสุ่มนี้

จากหลักการคูณ จะได้ว่า วิธีเลือกจำนวนสองจำนวนนี้ไม่ซ้ำกันจาก {1,2,3,4,5} ทั้งหมด  5 x 4 = 20 วิธี 
ดังนั้น n(s) = 20

ให้ E แทนเหตุการณ์ที่จะได้จำนวนแรกมากกว่า 3 และจำนวนทั้งสองไม่ซ้ำกัน

หาจำนวนสมาชิก E ได้ดังนี้

ขั้นที่ 1 เลือกจำนวนแรกได้ 2 วิธี เลือก 4 หรือ 5

ขั้นที่ 2 ในแต่ละวิธีของขั้นที่ 1 จะมีวิธีเลือกจำนวนที่สองที่ไม่ซ้ำกับจำนวนแรกได้ 4 วิธี 

ดังนั้น n(E) = 2 x 4 = 8

จะได้  P(E) = n(E)n(s) = 820 = 25 ( ใส่รูป 2 )

ดังนั้น ความน่าจะเป็นที่จะได้จำนวนแรกมากกว่า 3 เท่ากับ 2/5

---

กฎที่สำคัญบางประการของความน่าจะเป็น

ปริภูมิตัวอย่างและเหตุการณ์ต่างก็เป็นเซต โดยในที่นี้ เอกภพสัมพัทธ์คือปริภูมิตัวอย่าง ซึ่งมีเหตุการณ์เป็นสับเซต ดังนั้น สมบัติพื้นฐานของความน่าจะเป็นได้มาจากสมบัติของการดำเนินการของเซต

ให้ S  = ปริภูมิตัวอย่างของการทดลองสุ่มหนึ่ง 

A , B = เหตุการณ์ 

นั่นคือ  A S  และ B S

จะได้ A B เป็นเหตุการณ์ที่ประกอบด้วยสมาชิกในเหตุการณ์ A หรือ เหตุการณ์ B หรือ ทั้งสองเหตุการณ์ 

นั่นคือ      A B = { x I x A หรือ x B}

ทฤษฎีบท

ให้ S เป็นปริภูมิตัวอย่างซึ่งเป็นเซตจำกัด และ A,B เป็นเหตุการณ์ใด ๆ จะได้ว่า

1. P(A U B) = P(A) + P(B) – P(AB)
2. ถ้า A B = แล้ว P(A U B) = P(A) + P(B)
3. P(A’) = 1 – P(A)
4. P(A-B) = P(A) – P(AB)

---

แบบฝึกหัด ความน่าจะเป็น ม.5

1.  ในการทอดลูกเต๋าเที่ยงตรงสองลูกพร้อมกันหนึ่งครั้ง จงหาความน่าจะเป็นของเหตุการณ์ที่

1. ลูกเต๋าทั้งสองลูกขึ้นแต้มเท่ากันหรือผลบวกของแต้มมากว่า 10
2. ลูกเต๋าทั้งสองลูกขึ้นแต้มเท่ากันหรือผลบวกของแต้มเป็น 7
3. ลูกเต๋าทั้งสองลูกขึ้นแต้มไม่เท่ากัน
4. ลูกเต๋าทั้งสองลูกขึ้นแต้มเท่ากันแต่ผลบวกของแต้ไม่มากกว่า 10

วิธีทำ
แทน S แทนปริภูมิตัวอย่างของการทดลองสุ่มนี้

A แทนเหตุการณ์ที่ลูกเต๋าทั้งสองขึ้นแต้มเท่ากัน

B แทนเหตุการณ์ที่ผลบวกของแต้มบนหน้าลูกเต๋าทั้งสองเป็น 7 

และ C แทนเหตุการณ์ที่ผลบวกของแต้มบนหน้าลูกเต๋าทั้งสองมากกว่า 10 

จะได้ 
S = {(1,1),(1,2),(1,3), (1,4),(1,5),(1,6),

(2,1),(2,2),(2,3), (2,4),(2,5),(2,6)

(3,1),(3,2),(3,3), (3,4),(3,5),(3,6)

(4,1),(4,2),(4,3), (4,4),(4,5),(4,6)

(5,1),(5,2),(5,3), (5,4),(5,5),(5,6)

(6,1),(6,2),(6,3), (6,4),(6,5),(6,6)}

A = {(1,1),(2,2),(3,3), (4,4),(5,5),(6,6)}

B = {(1,6),(2,5),(3,4), (4,3),(5,2),(6,1)}

C = {(5,6),(6,5),(6,6)}

---

[สรุปความน่าจะเป็น ม.6]

ความหมายและชนิดของตัวแปรสุ่ม

ตัวแปรสุ่ม (Random Variable) คือ ฟังก์ชันจากปริภูมิตัวอย่างของการทดลองสุ่มไปยังเซตของจำนวนจริง

โดยทั่วไป ตัวแปรสุ่มแบ่งได้เป็น 2 ชนิด ตามลักษณะของค่าที่เป็นไปได้ของตัวแปรสุ่ม

1. ตัวแปรสุ่มไม่ต่อเนื่อง คือ ตัวแปรสุ่มที่ค่าที่เป็นไปได้ทั้งหมดอยู่ในเซตที่สามารถนับจำนวนสมาชิกได้ หรือ ค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่มสามารถเขียนเรียงลำดับจากน้อยไปมากได้ ทั้งนี้เซตค่าของที่เป็นไปได้อาจเป็นเซตจำกัดหรือเซตอนันต์ก็ได้

ตัวอย่าง

ในการทอดลูกเต๋า 2 ลูก พร้อมกัน 1 ครั้ง ถ้าให้ตัวแปรสุ่มคือผลบวกของแต้มบนหน้าลูกเต๋าทั้งสองจะได้เซตของค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่ม คือ {2,3,4,5,6,7,8,9,10,11,12}

ในการโยนเหรียญ 1 เหรียญ 1 ครั้ง ถ้าได้ตัวแปรสุ่มเป็น 0 เมื่อเหรียญขึ้นหัว และ 1 เมื่อเหรียญขึ้นก้อย จะได้เซตของค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่ม คือ {0,1}

2. ตัวแปรสุ่มต่อเนื่อง คือ ตัวแปรสุ่มที่เซตของค่าที่เป็นไปได้ทั้งหมดเป็นสับเซตของ R

ตัวอย่าง

ให้ตัวแปรสุ่มคือความสูงของนักเรียนชั้นม.6 ห้องหนึ่ง อาจได้ว่าเซตของค่าที่เป็นไปได้ทั้งหมด ของตัวแปรสุ่มเป็นช่วง [150,190]

ให้ตัวแปรสุ่มคือน้ำหนักของแตงโม ที่เกี่ยวกับได้จากสวนแห่งหนึ่ง อาจได้ว่าเซตของค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่มเป็นช่วง [1,6]

การแจกแจงความน่าจะเป็นของตัวแปรสุ่มไม่ต่อเนื่อง

การหาความน่าจะเป็นของตัวแปรสุ่มที่สนใจสามารถใช้ความรู้เรื่องความน่าจะเป็นที่เรียนมาแล้วในชั้นม.5 และสามารถหาได้จากความถี่สัมพัทธ์จากตารางความถี่ได้อีกด้วยดังตัวอย่างต่อไปนี้ 

ตัวอย่างที่ 1 

จำนวนพี่น้องของนักเรียนชั้นมัธยมศึกษาปีที่ 6 ห้องหนึ่งจำนวน 50 คนแสดงด้วยตารางความถี่ได้ดังนี้ 

ถ้าสุ่มนักเรียน 1 คนจากห้องนี้และให้ตัวแปรสุ่ม x คือจำนวนพี่น้องของนักเรียนที่สุ่ม ได้จงหาความน่าจะเป็นที่นักเรียนที่สุ่มได้จะมีพี่น้อง x คนเมื่อ x {0,1,2,3,4}

วิธีทำ     สำหรับ  x {0,1,2,3,4} จะได้ว่า P(X=x) คือ ความน่าจะเป็นที่นักเรียนที่สุ่มได้จะมีพี่น้อง x คน 

ดังนั้น     P(X=0) = 6/50 = 0.12

 P(X=1) = 22/50 = 0.44

 P(X=2) = 17/50 = 0.34

 P(X=3) = 4/50 = 0.08

 P(X=4) = 1/50 = 0.02

จากตัวอย่างข้างต้นจะเห็นว่าความน่าจะเป็นของการเกิดค่าแต่ละค่าที่เป็นไปได้ของตัวแปรสุ่มคือ
ความถี่สัมพัทธ์ 

โดยทั่วไปสำหรับตัวแปรสุ่ม x ใด ๆ จะได้ 0 น้อยกว่าหรือเท่ากับ P(X=x)  น้อยกว่าหรือเท่ากับ 1
และผลรวมของความน่าจะเป็นของการเกิดค่าแต่ละค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่มเท่ากับ 1

---

การแจกแจงเอกรูปไม่ต่อเนื่อง

บทนิยาม 

ให้ x เป็นตัวแปรสุ่มไม่ต่อเนื่องถ้าค่าที่เป็นไปได้ทั้งหมดของ x คือ X₁ , X₂ , X₃ , ….X_n

แล้วการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม X เป็น การแจกแจงเอกรูปไม่ต่อเนื่อง
เมื่อ P(X=x₁) = 1/n สำหรับทุก i {1,2,3,…..,n}

จากบทนิยามจะเห็นว่าการแจกแจงความน่าจะเป็นของตัวแปรสุ่มจะเป็นการแจกแจงเอกรูปไม่ต่อเนื่องเมื่อเกิดค่าแต่ละค่าที่เป็นไปได้ของตัวแปรสุ่มมีความน่าจะเป็นเท่ากัน 

ความน่าจะเป็น ตัวอย่าง 

ในการทอดลูกเต๋าที่เที่ยงตรง 1 ลูก 1 ครั้งให้ตัวแปรสุ่ม x คือแต้มบนหน้าลูกเต๋าจงพิจารณาว่าการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม x เป็นการแจกแจงเอกรูปไม่ต่อเนื่องหรือไม่พร้อมทั้งเขียนแสดงการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม x ในรูปตารางและกราฟ 

วิธีทำ 
ค่าที่เป็นไปได้ของตัวแปรสุ่ม X คือ 1,2,3,4,5 และ 6

สำหรับ x {1,2,3,4,5,6} จะได้ว่า P(X=x) คือความน่าจะเป็นที่ลูกเต๋าขึ้นแต้ม x

เนื่องจากลูกเต๋าเที่ยงตรง จะได้ว่า P(X=x) = ⅙
ดังนั้น การแจกแจงความน่าจะเป็นของตัวแปรสุ่ม X เป็นการแจกแจงเอกรูปไม่ต่อเนื่อง
จะได้ตารางแสดงการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม X ดังนี้

และได้กราฟแสดงการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม X ดังนี้

---

การแจกแจงทวินาม

การแจกแจงทวินาม คือ การแจกแจงความน่าจะเป็นของตัวแปรสุ่ม x ซึ่งคือจำนวนครั้งของการเกิดผลสำเร็จจากการทดลองสุ่ม n ครั้งที่เป็นอิสระการ โดยในแต่ละครั้งมีโอกาสเกิดผลสำเร็จด้วยความน่าจะเป็นเท่ากับ p และไม่เกิดผลสำเร็จด้วยความน่าจะเป็นเท่ากับ 1 – p

หมายเหตุ

1. เรียก n และ p ว่าพารามิเตอร์ของการแจกแจงทวินามและเขียนสัญลักษณ์  X ~ B (n,p) เพื่อแสดงว่าการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม x เป็นการแจกแจงทวินามที่มี n และ p เป็นพารามิเตอร์ 
2. การทดลองสุ่ม 1 ครั้งจะมีผลลัพธ์ที่เป็นไปได้ 2 แบบคือสำเร็จหรือไม่สำเร็จเรียกว่า  การลองแบร์นูลลี เช่นการโยนเหรียญ 1 เหรียญ 1 ครั้ง 

สรุปลักษณะการแจกแจงทวินาม

1. เกิดจากการทดลองสุ่มจำนวน n ครั้งที่เป็นอิสระการกล่าวคือผลที่ได้จากการทดลองสุ่มในครั้งก่อนหน้าไม่ส่งผลต่อการทดลองสุ่มในครั้งต่อไป 
2. การทดลองสุ่มแต่ละครั้งมีผลลัพธ์ที่เป็นไปได้เพียง 2 แบบคือสำเร็จหรือไม่สำเร็จ 
3. ความน่าจะเป็นที่จะเกิดผลสำเร็จในการทดลองส่งแต่ละครั้งเท่ากันให้เป็น p เมื่อ 0 < p < 1 และจะได้ความน่าจะเป็นที่จะไม่เกิดผลสำเร็จในการทดลองสุ่มแต่ละครั้งเป็น  1-p

ทฤษฎีบท

ถ้าการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม x เป็นการแจกแจงทวินามจะได้ว่า ( ใส่รูป 4 )

เมื่อ n แทนจำนวนครั้งของการทดลองสุ่ม และ p แทนความน่าจะเป็นที่จะเกิดผลสำเร็จ
ในการทดลองสุ่มแต่ละครั้ง

ตัวอย่าง 

1. จากข้อมูลเกี่ยวกับคุณภาพของสินค้าซึ่งเก็บรวบรวมมาในอดีตทำให้ทราบว่าความน่าจะเป็นที่สินค้าแต่ละชิ้นจะชำรุดเป็น 0.05 และในกระบวนการตรวจสอบคุณภาพสินค้าของโรงงานมีหลักการคือพนักงานจัดส่งสินค้าจำนวน 5 ชิ้นจากแต่ละกล่องเพื่อตรวจสอบคุณภาพถ้าตรวจพบสินค้าชำรุดไม่เกิน 1 ชิ้นสินค้ากล่องนั้นจะผ่านการตรวจสอบคุณภาพ 

จงหาว่าความน่าจะเป็นที่สินค้าแต่ละกล่องที่ส่งมาตรวจสอบจะผ่านการตรวจสอบคุณภาพ

วิธีทำ

ให้ตัวแปรสุ่ม x คือจำนวนสินค้าที่ชำรุดเมื่อส่งสินค้า 5 ชิ้นจากแต่ละกล่องจะได้ค่าที่เป็นไปได้ของตัวแปรสุ่ม x คือ 0,  1 , 2,  3,  4,  5  

ความน่าจะเป็นของที่สินค้าแต่ละกล่องที่ส่งมาตรวจสอบจะผ่านการตรวจสอบคุณภาพคือ 

P (X น้อยกว่าหรือเท่ากับ 1) = P(X=0) + P(X=1)

= (50) (0.95)⁵ +  (51)(0.05)(0.95)⁴

  0.7738 + 0.2036

0.9774

---

การแจกแจงความน่าจะเป็นของตัวแปรสุ่มต่อเนื่อง

กรณีที่ตัวแปรสุ่มที่สนใจเป็นตัวแปรสุ่มต่อเนื่อง ซึ่งมีเซตของค่าที่เป็นไปได้ทั้งหมดเป็นช่วง ซึ่งเป็นสับเซตของ R ซึ่งมีจำนวนสมาชิกเป็นอนันต์ จึงไม่เหมาะที่จะเขียนแจกแจงในรูปตาราง

แต่จะใช้เป็น เส้นโค้งความหนาแน่น โดยความน่าจะเป็นที่ตัวแปรสุ่มจะมีค่าอยู่ในช่วงใดช่วงหนึ่งจะเท่ากับพื้นที่ปิดล้อมด้วยเส้นโค้งความหนาแน่นกับแกน X ในช่วงนั้น เรียกพื้นที่ดังกล่าวว่า พื้นที่ใต้เส้นโค้งความหนาแน่น

เส้นโค้งความหนาแน่นเป็นกราฟของฟังก์ชัน y = f(x) โดยที่ x แทนค่าที่เป็นไปได้ของตัวแปรสุ่ม เรียกฟังก์ชันนี้ว่า ฟังก์ชันความหนาแน่นความน่าจะเป็น

การแจกแจงปกติ

การแจกแจงปกติ คือ การแจกแจงความน่าจะเป็นของตัวแปรสุ่มต่อเนื่อง X ที่มีฟังก์ชันความหนาแน่นความน่าจะเป็น คือ ( ใส่รูป 5 )

การแจกแจงปกติมาตรฐาน

คือ การแจกแจง ปกติที่มีค่าเฉลี่ยเท่ากับ 0 ( =0) และส่วนเบี่ยงเบนมาตรฐานเท่ากับ 1 ( = 1)

เรียกเส้นโค้งปกติซึ่งได้จากตัวแปรสุ่มปกติที่มีค่าเฉลี่ยเป็น 0 และส่วนเบี่ยงเบนมาตรฐานเป็น 1 ว่า เส้นโค้งปกติมาตรฐาน ดังรูป

เรียกตัวแปรสุ่มที่มีการแจกแจงปกติมาตรฐานว่า ตัวแปรสุ่มปกติมาตรฐาน

---

ความน่าจะเป็น สูตร ทั้งหมดที่ควรจำได้

สูตรความน่าจะเป็น สุ่มหยิบ

1. กฎการนับเบื้องต้น

กฎการคูณ : จำนวนวิธีของงานที่ยังไม่เสร็จ = จำนวนวิธีในแต่ละขั้นตอนคูณกัน  

กฎการบวก : จำนวนวิธีของงานที่ทำเสร็จแล้ว= จำนวนวิธีของแต่ละกรณีมาบวกกัน 

2.สัญลักษณ์ Factorial (!) , Combination ( C nr ) และ Permutation ( P nr )  ( ใส่รูป 6 )

3. วิธีเรียงสับเปลี่ยน (Permutation) คือ การนำสิ่งของมาจัดเรียงกันโดยคำนึงถึงตำแหน่ง เป็นสำคัญ

• การเรียงแบบเชิงเส้น การนำสิ่งของ n สิ่งที่แตกต่างกันทั้งหมดมาจัดเรียงเป็นแนวเส้นตรงคราวละ
  n สิ่งจะได้ n! วิธี
• การนำสิ่งของ n สิ่งที่แตกต่างกันทั้งหมดมาจัดเรียงเป็นแนวเส้นตรงคราวละ r สิ่ง (เลือกมาเรียง)
  จะได้ P nr  วิธี
• การเรียงแบบวงกลม การนำสิ่งของ n สิ่งที่แตกต่างกันทั้งหมดมาจัดเรียงเป็นวงกลมคราวละ
  n สิ่งจะได้ n 1! วิธี

4. วิธีจัดหมู่ (Combination) คือ การเลือกของ บางสิ่งหรือทั้งหมดของจำนวนหนึ่งที่มีอยู่โดย ตำแหน่งหรือลำดับไม่มี ความสำคัญ ไม่สนใจลำดับการเลือกของ r สิ่งจากของ n สิ่งที่แตกต่างกัน จะได้ C nr วิธี

5. การแบ่งของ : การแบ่งของแตกต่างกันออกเป็นกลุ่มย่อย ๆ
( ใส่รูป 7 )

คำถามที่พบบ่อย (FAQ)